How to approximate function for geometrically growing sequence?-CodePudding

I have the function to create x0:

x0 = []
    for i in range(0,N):
        if i == 0:
            a =  0.4
        else:
            a = round(0.4   0.3*2**(i-1), 1)
        print(i, a)
        x0.append(a)

which gives me data of growing sequence: [0.4, 0.7, 1.0, 1.6, 2.8, 5.2, 10.0, 19.6, 38.8, 77.2, ...] which I want to find a function to fit to these points. I don't want to use polynomials because the N can be different but need to find single parameter function. The projection needs to be very general.

My approach is using the code:

def fun(x, a, b):    
    return np.cos(x**(2/3) * a   b) 
    
# Make fit #
y0 = [0]*len(x0)
p, c = curve_fit(f=fun, xdata=np.array(x0), ydata=y0)
  
x = np.linspace(0, max(x0), 10000)    
plt.plot(x, fun(x, *p))    
plt.scatter(x0, y0)

That function's progress seem to be too wide for starting points and quite fit the last ones. I also tried to lower the initial oscillations by multiplying this function by x, but the period still is too wide at the beginning. Is it possible to find good oscillation function to go thru (almost) all those points? I don't know how to set parameter under the x**(...) because placing there a variable cause the fit to estimate it as close to 1, which is not what I need. Can I set the power for sin(x**b) that way? If not what functions family should I try?

Below the plot for function multiplied by b*x. The oscillations at first points should be much denser.

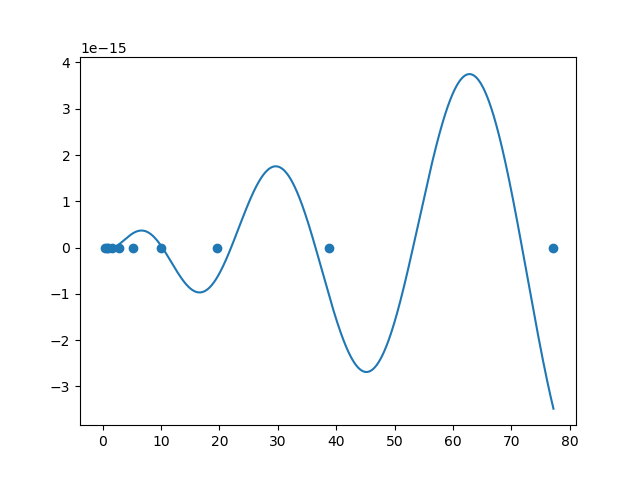
CodePudding user response：

Thanks to suggestions I've found the best fit and I think it can't be better.

The solution is:

 def fun(x, a, b, c):
        return np.cos(np.pi*(np.log2((x-a)/b)   c))

and the fit method looks like

p, c = curve_fit(f=fun, xdata=np.array(x0), ydata=y0, bounds=([0, -np.inf, -np.inf], [x0[0], np.inf, np.inf]))

It's important to set initial bounds for a to avoid convergention failure or "Residuals are not finite in the initial point" issues. At last each point has its own crossing despite mad behavior of the close to 0 at the domain. Parameters are pretty close to 0 or 1 - not tending to infinity.