R: Customizing the Travelling Salesman Problem-CodePudding

I am working with the R programming language.

I found this (very good) tutorial that shows how to implement the Genetic Algorithm for the Travelling Salesman Problem (for a set of European cities) in R: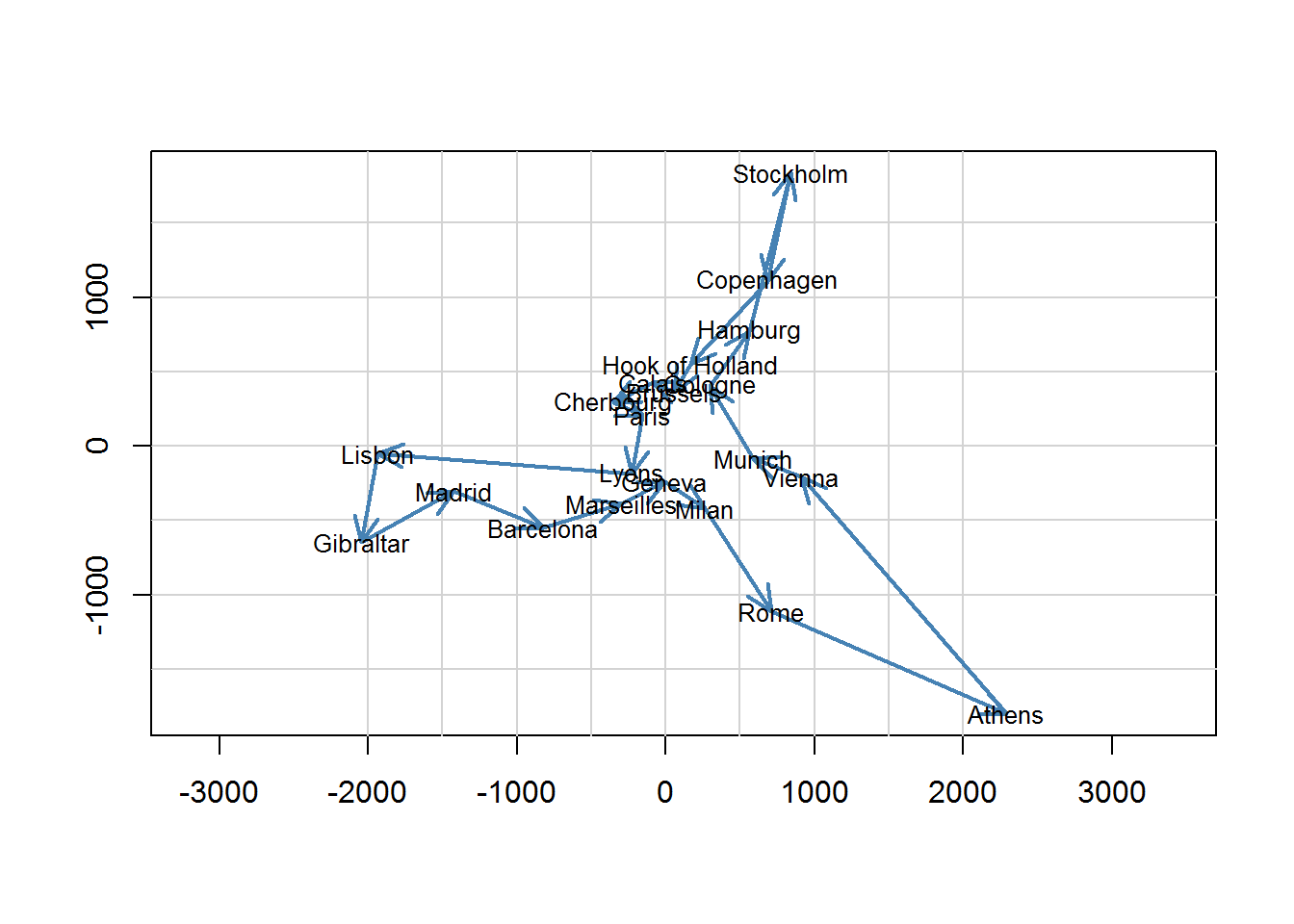

My Question:

Is it possible to "customize" this problem by adding some constraints? For instance, suppose you absolutely want to start your trip in Vienna - is there a way to tell the Genetic Algorithm to begin searching for the optimal path with the first city being Vienna?
Is it possible to instruct the Genetic Algorithm to have certain cities in certain positions? For example, you want the first city to be Vienna and the sixth city to be Athens - and then, search for the optimal path given these constraints?

Is it possible to customize the Genetic Algorithm in R to take these "considerations" into account when optimizing the Travelling Salesman Problem?

CodePudding user response：

To expand on my comment. When dealing with constraints in genetic algorithm you have two options:

incorporate conditions in fitness function
insure that genetic operators create feasible solutions

With first approach you need to decide what to do with infeasible solutions (ex. penalization) and that is extremely problem dependent. If conditions are hard to achieve most of the solutions that evolutionary algorithm creates in the process will be infeasible and it will cause premature convergence.

Which approach to adapt is problem dependent, I'll show you how to implement 2nd approach for this problem.

matrix transformation:

transformMatrix <- function(fixed_points, D){
  
  if(length(fixed_points) == 0) return(D)
  
  p <- integer(nrow(D))
  pos <- match(names(fixed_points), colnames(D))
  p[fixed_points] <- pos 
  p[-fixed_points] <- sample(setdiff(seq_len(nrow(D)), pos))

  D[p, p]
}

goal of this function is to permute rows and columns of matrix to get cities to their specified positions:

fixed_points <- c(
  "Vienna" = 1,
  "Athens" = 6
)
D_perm <- transformMatrix(fixed_points, D)

feasible initial population

feasiblePopulation <- function(n, size, fixed_points){
  
  positions <- setdiff(seq_len(n), fixed_points)
  
  m <- matrix(0, size, n)
  if(length(fixed_points) > 0){
    
    m[, fixed_points] <- rep(fixed_points, each = size)
    
    for(i in seq_len(size))
      m[i, -fixed_points] <- sample(positions)
    
  } else {
    
    for(i in seq_len(size))
      m[i,] <- sample(positions)
  }
  
  m
}

this function creates feasible solutions

mutation

mutation <- function(n, fixed_points){
  
  positions <- setdiff(seq_len(n), fixed_points)
  
  function(obj, parent){
    
    vec <- obj@population[parent,]
    if(length(positions) < 2) return(vec) 
    
    indices <- sample(positions, 2)
    replace(vec, indices, vec[rev(indices)])
  }
}

we need to ensure that mutation operator keeps fixed positions in place. This function returns one such mutation operator.

fitness function

fitness <- function(tour, distMatrix) {
  
  tour <- c(tour, tour[1])
  route <- embed(tour, 2)[,2:1]
  1/sum(distMatrix[route])
}

We want to minimize distance hence taking the reciprocal.

optimization step

res <- ga(
  type = "permutation",
  fitness = fitness,
  distMatrix = D_perm,
  lower = 1,
  upper = nrow(D_perm),
  mutation = mutation(nrow(D_perm), fixed_points),
  crossover = gaperm_pmxCrossover,
  suggestions = feasiblePopulation(nrow(D_perm), popSize, fixed_points),
  popSize = popSize,
  maxiter = 5000,
  run = 500,
  pmutation = 0.2
)

gaperm_pmxCrossover will insure that fixed positions stay fixed during the crossover process (that is why I didn't write custom crossover operator)

solution (city order)

colnames(D_perm)[res@solution[1,]]

Also first city is last (route)