Eigenvectors and samples to calculate the points on PCA scale-CodePudding

I want to get the new points on the new scale for PC1 and PC2. I calculated the Eigenvalues, Eigenvectors and Contribution.

Now I want to calculate the points on the new scale (scores) to apply the K-Means cluster algorithm on them.

Whenever I try to calculate it by saying z_new = np.dot(v, vectors) (with v = np.cov(x)) I get a wrong score, which is [[14. -2. -2. -1. -0. 0. 0. -0. -0. 0. 0. -0. 0. 0.] for PC1 and [-3. -1. -2. -1. -0. -0. 0. 0. 0. -0. -0. 0. -0. -0.] for PC2. The right score scores (Calculated using SciKit's PCA() function) should be PC1: [ 4 4 -6 3 1 -5] and PC2: [ 0 -3 1 -1 5 -4]

Here is my code:

dataset = pd.read_csv("cands_dataset.csv")
x = dataset.iloc[:, 1:].values

m = x.mean(axis=1);
for i in range(len(x)):
    x[i] = x[i] - m[i]

z = x / np.std(x)
v = np.cov(x)
values, vectors = np.linalg.eig(v)
d = np.diag(values)
p = vectors
z_new = np.dot(v, p) # <--- Here is where I get the new scores
z_new = np.round(z_new,0).real
print(z_new)

The result I get:

[[14. -2. -2. -1. -0.  0.  0. -0. -0.  0.  0. -0.  0.  0.]
 [-3. -1. -2. -1. -0. -0.  0.  0.  0. -0. -0.  0. -0. -0.]
 [-4. -0.  3.  3.  0.  0.  0.  0.  0. -0. -0.  0. -0. -0.]
 [ 2. -1. -2. -1.  0. -0.  0. -0. -0.  0.  0. -0.  0.  0.]
 [-2. -1.  8. -3. -0. -0. -0.  0.  0. -0. -0. -0.  0.  0.]
 [-3.  2. -1.  2. -0.  0.  0.  0.  0. -0. -0.  0. -0. -0.]
 [ 3. -1. -3. -1.  0. -0.  0. -0. -0.  0.  0. -0.  0.  0.]
 [11.  6.  4.  4. -0.  0. -0. -0. -0.  0.  0. -0.  0.  0.]
 [ 5. -8.  6. -1.  0.  0. -0.  0.  0.  0.  0. -0.  0.  0.]
 [-1. -1. -1.  1.  0. -0.  0.  0.  0.  0.  0.  0. -0. -0.]
 [ 5.  7.  1. -1.  0. -0. -0. -0. -0.  0.  0. -0. -0. -0.]
 [12. -6. -1.  2.  0.  0.  0. -0. -0.  0.  0. -0.  0.  0.]
 [ 3.  6.  0.  0.  0. -0. -0. -0. -0.  0.  0.  0. -0. -0.]
 [ 5.  5. -0. -4. -0. -0. -0. -0. -0.  0.  0. -0.  0.  0.]]

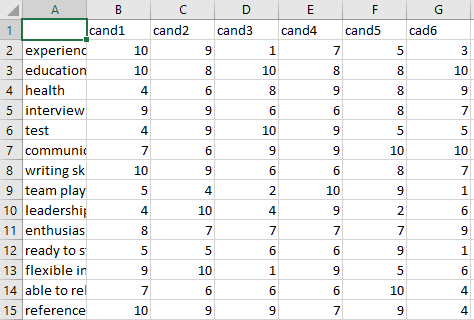
Dataset(Requested by a comment):

CodePudding user response：

The way I look at this, you have 6 samples with 14 dimensions. The PCA procedure is as follows:

1. Remove the mean

Starting with the following data:

data  = np.array([[10, 9, 1, 7, 5, 3],
                  [10, 8,10, 8, 8,10],
                  [ 4, 6, 8, 9, 8, 9],
                  [ 9, 9, 6, 6, 8, 7],
                  [ 4, 9,10, 9, 5, 5],
                  [ 7, 6, 9, 9,10,10],
                  [10, 9, 6, 6, 8, 7],
                  [ 5, 4, 2,10, 9, 1],
                  [ 4,10, 4, 9, 2, 6],
                  [ 8, 7, 7, 7, 7, 9],
                  [ 5, 5, 6, 6, 9, 1],
                  [ 9,10, 1, 9, 5, 6],
                  [ 7, 6, 6, 6,10, 4],
                  [10, 9, 9, 7, 9, 4]])

We can remove the mean via:

centered_data = data - np.mean(data, axis=1)[:, None]

2. Create a covariance matrix

Can be done as follows:

covar = np.cov(centered_data)

3. Getting the Principal Components

This can be done using eigenvalue decomposition of the covariance matrix

eigen_vals, eigen_vecs = np.linalg.eig(covar)
eigen_vals, eigen_vecs = np.real(eigen_vals), np.real(eigen_vecs)

4. Dimensionality redunction

Now we can do dimensionality reduction by choosing the two PC with the highest matching eigenvalues (variance). In your example you wanted 2 dimension so we take the two major PCs:

eigen_vals = 
array([ 3.34998559e 01,  2.26499704e 01,  1.54115835e 01,  9.13166675e 00,
        1.27359015e 00, -3.10462438e-15, -1.04740277e-15, -1.04740277e-15,
       -2.21443036e-16,  9.33811755e-18,  9.33811755e-18,  6.52780501e-16,
        6.52780501e-16,  5.26538300e-16])

We can see that the first two eigen values are the highest:

eigen_vals[:2] = array([33.49985588, 22.64997038])

Therefore, we can project the data on the two first PCs as follows:

projected_data = eigen_vecs[:, :2].T.dot(centered_data)

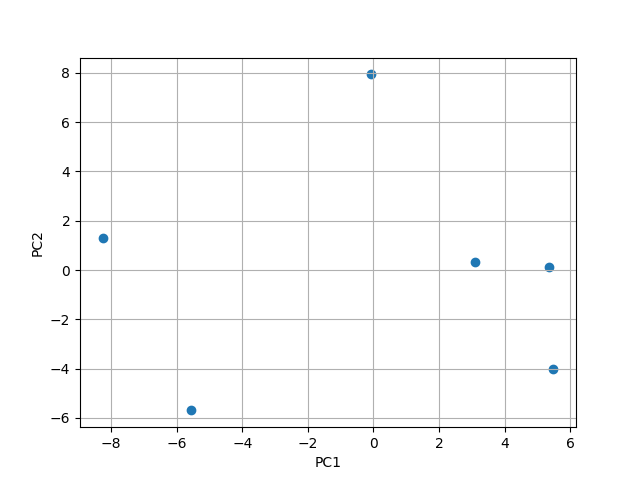
This can now be scaterred and we can see that the 14 dimension are reduced to 2:

PC1 = [0.59123632, -0.10134531, -0.20795954,  0.1596049 , -0.07354629, 0.19588723,  0.19151677,  0.33847213,  0.22330841, -0.03466414, 0.1001646 ,  0.52913917,  0.09633029,  0.16141852]
PC2 = [-0.07551251, -0.07531288,  0.0188486 , -0.01280896, -0.07309957, 0.12354371, -0.01170589,  0.49672196, -0.43813664, -0.09948337, 0.49590461, -0.25700432,  0.38198034,  0.2467548 ]

General analysis

Since we did PCA wee now have orthogonal variance in each dimension (diagonal covariance matrix). to better understand the dimensionality reduction possible we can see how the total variance of the data is distributed in the different dimensions. This can be dome via the eigenvalues:

var_dim_contribution = eigen_vals / np.sum(eigen_vals)

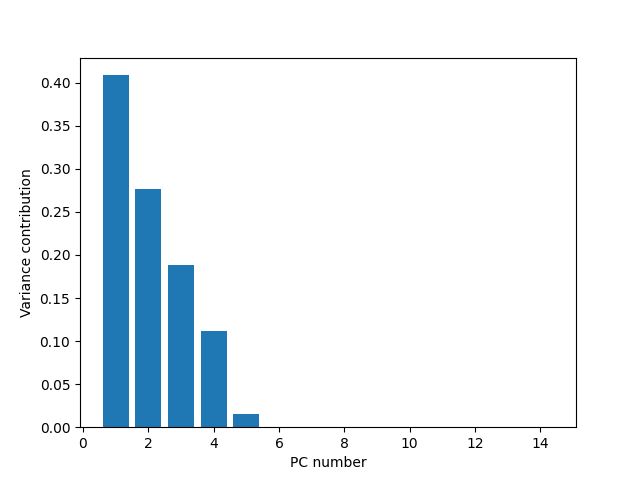
Plotting this results in:

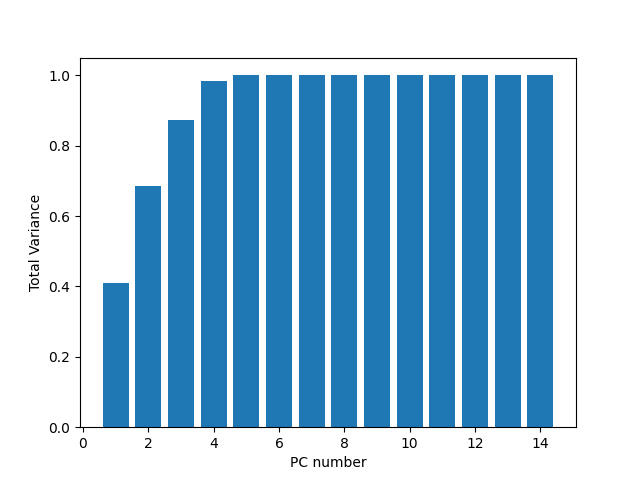
We can see here that using the 2 major PCs we can describe ~67% of the variance. Adding a third dimension will boost us towards ~90% of the variance. This is a good reduction from 14. This can be better seem in the cumulative variance plot.

var_cumulative_contribution = np.cumsum(eigen_vals / np.sum(eigen_vals))

Comparison with sklearn

When comparing with sklearn.decomposition.PCA we get the following:

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(centered_data.T)
print(pca.explained_variance_ratio_)  # [0.40870097 0.27633148]
print(pca.explained_variance_)        # [33.49985588 22.64997038]

We see that we get the same explained variance and variance values as the ones from the manual computation, In addition, The resulted PCs are:

print(pca.components_)
[[-0.59123632  0.10134531  0.20795954 -0.1596049   0.07354629  0.19588723 0.19151677 -0.33847213 -0.22330841  0.03466414 -0.1001646  -0.52913917 -0.09633029 -0.16141852]
 [-0.07551251 -0.07531288  0.0188486  -0.01280896 -0.07309957  0.12354371 -0.01170589  0.49672196 -0.43813664 -0.09948337  0.49590461 -0.25700432 0.38198034  0.2467548 ]]

And we see that we get the same results as scikit