I am debugging some VBA code and I have an IIF function which I don't understand what is doing. It's IIF(constant And i, "TRUE", "FALSE"), where I gets values from 0 to n.
I know that this function is equivalent to IF in Excel. But in this case what is the condition? What does the expression number and number means? I run this sample:
Sub Sample()
For i = 0 To 20
Cells(i 1, 1) = i
Cells(i 1, 2) = 4 And i
Next i
End Sub
And I get the values below:
CodePudding user response:
The expression 4 And i will do an arithmetic AND-operation. Example:
6: 0 0 0 0 0 1 1 0
4: 0 0 0 0 0 1 0 0
Result: 0 0 0 0 0 1 0 0
11: 0 0 0 0 1 0 1 1
4: 0 0 0 0 0 1 0 0
Result: 0 0 0 0 0 0 0 0
So 6 AND 4 is 4 while 11 AND 4 is 0.
Now 0 is seen as False and everything not 0 is seen as True. Used in an IIF-statement, all numbers that have the 3rd bit (counting from right) set will execute the True-part of the IIF, all others the False.
CodePudding user response:
Your And operator does a bit wise comparison:
result = expression1 And expression2
When applied to numeric values, the And operator performs a bitwise comparison of identically positioned bits in two numeric expressions and sets the corresponding bit in result according to the following table.
| If bit in expression1 is | And bit in expression2 is | The bit in result is |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Since the logical and bitwise operators have a lower precedence than other arithmetic and relational operators, any bitwise operations should be enclosed in parentheses to ensure accurate results.
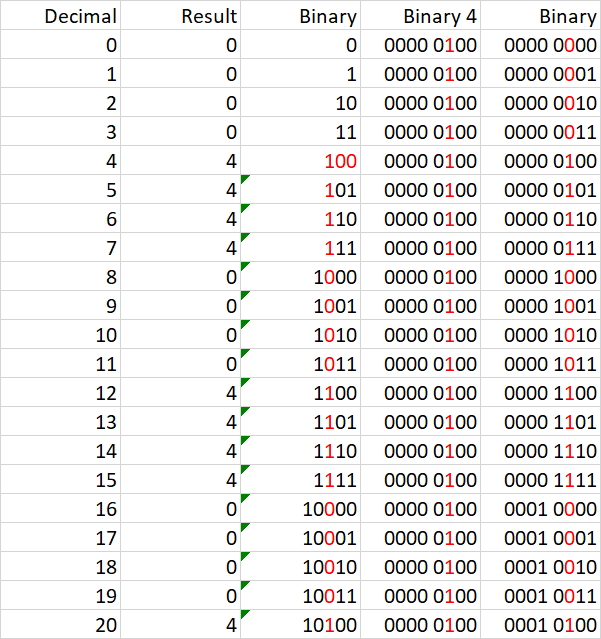
So converting the 4 into binary it results in 100. I have done that in the 3ʳᵈ column below, where I converted all numbers of the 1ˢᵗ column to binaries. The other 2 columns are just filled up with zeros for better visibility:
So watching the table above you only get a 1 as result if both bits in the same position are a 1 otherwise you get a 0. That means you always get a 4 as result if 4 and i has a 1 in the 3ʳᵈ bit from the right due to the bitwise comparison (see the red bits).