I could not understand and think of a scenario when a search operation in an imbalanced binary search tree could be more efficient than in a balanced binary search tree. If the binary search tree is highly skewed, then it might take the form of a linked list at which time, the run time complexity will be O(n). Is there any scenario where it can really happen? My professor insisted that there are some but I simply cannot think of any.

CodePudding user response：

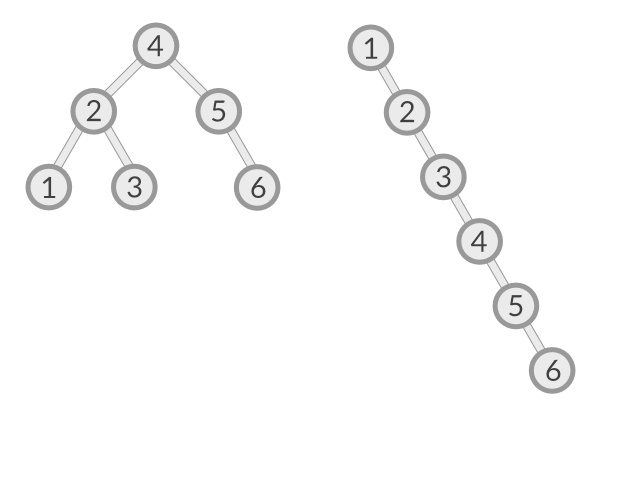
There are some cases where an imbalanced tree could be better. Take the following two trees as an example:

The idea behind a binary search tree is that if you're equally likely to search for any of the values in the set of nodes, then keeping the tree balanced minimizes the average number of comparisons you have to do.

For example, if I search for each of the values (1, 2, 3, 4, 5, 6), then I'd want to be searching the balanced tree on the left. Performing that sequence of searches on the balanced tree would result in (3 2 3 1 2 3) = 14 comparisons. Doing the same sequence of searches on the unbalanced tree would result in (1 2 3 4 5 6) = 21 comparisons.

But what if I knew that the values I need to search for weren't going to be evenly distributed, but that they skewed low? What if I wanted to search for the values (1, 2, 1, 2, 1, 3)? Which tree would give better performance then?

Performing those searches on the balanced tree would result in (3 2 3 2 3 3) = 16 comparisons. Not bad, but the same sequence of searches on the unbalanced tree would only take (1 2 1 2 1 3) = 10 comparisons.

This is a contrived example, but it shows that knowing your data and knowing the values that people are likely to search for most often can help you choose the right arrangement for that data to give better performance.