2D blocking with unique matrix transpose problem-CodePudding

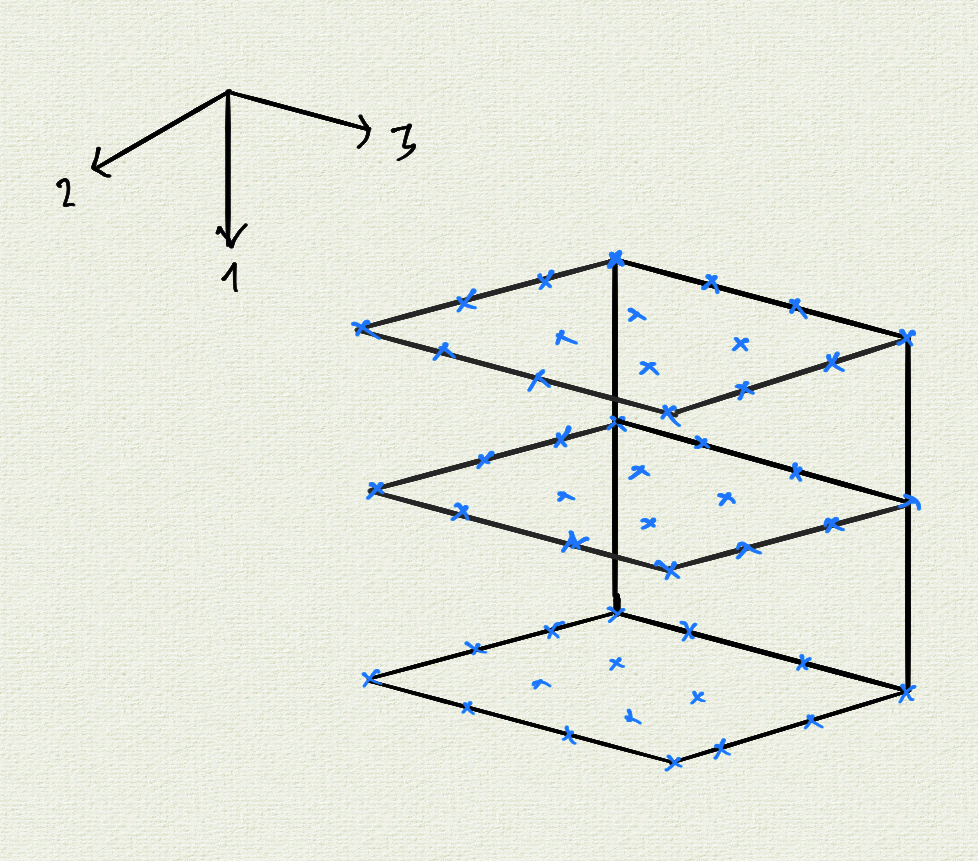
I have complex valued data of type struct complex {double real = 0.0; double imag = 0.0;}; organized in the form of an order-3 tensor. The underlying container has a contiguous memory layout aligned with the memory-page boundary.

The natural 'slicing' direction of the tensor is along direction 1. This means the cache-lines extend in directions 3, 2 and finally 1, in that order. In other words, the indexing function looks like this: (i, j, k) -> i * N2 * N3 j * N3 k.

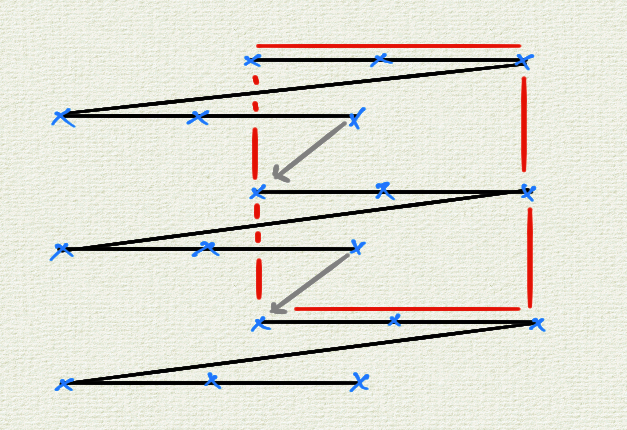
I am required to transpose the slices along direction 2. In the first of the above images, the rectangle in red is the slice of the tensor which I wish to have transposed.

My code in C looks like this:

for (auto vslice_counter = std::size_t{}; vslice_counter < n2;   vslice_counter)
    {        
        // blocked loop
        for (auto bi1 = std::size_t{}; bi1 < n1; bi1  = block_size)
        {
            for (auto bi3 = std::size_t{}; bi3 < n3; bi3  = block_size)
            {
                for (auto i1 = std::size_t{}; i1 < block_size;   i1)
                {
                    for (auto i3 = std::size_t{}; i3 < block_size;   i3)
                    {
                        const auto i1_block = bi1   i1;
                        const auto i3_block = bi3   i3;
                        tens_tr(i3_block, vslice_counter, i1_block) = tens(i1_block, vslice_counter, i3_block);
                    }
                }
            }
        }
    }

Machine used for testing: dual socket Intel(R) Xeon(R) Platinum 8168 with

24 cores @ 2.70 GHz and
L1, L2 and L3 caches sized 32 kB, 1 MB and 33 MB respectively.

I plotted the graph of the performance of this function w.r.t block-size but I was surprised to see that there is no variation! In fact, the naive implementation performs just as well as this one.

Question: Is there a reason why 2D blocking isn't helping boost the performance in this case?

Edit:

Additional information:

The compiler used is the Intel C compiler.
block_size is an input parameter and not a compile time constant.
During testing, I varied the value of block_size from 4 to 256. This translates to blocks of 256 B and 1 MB respectively since the blocks are squares of side-length block_size. My aim was to fill up the L1 and/or L2 caches with the blocks.
Compilation flags used for optimization: -O3;-ffast-math;-march=native;-qopt-zmm-usage=high

CodePudding user response：

TL;DR: the 2D blocking code is not faster mainly because of cache trashing (and a bit due to prefetching). Both the naive implementation and the 2D-blocking are inefficient. A similar effect is described in this post. You can mitigate this problem using small a temporary array and improve performance using a register-tiling optimization. Additional padding may also be helpful.

CPU Caches

First of all, modern CPU cache are set-associative cache. A m-way associative cache can be seen as a n x m matrix with n sets containing a block of m cache lines. Memory blocks are first mapped onto a set and then placed into any of the m cache line of a target set (regarding the cache replacement policy). When an algorithm (like a transposition) performs strided memory accesses, the processor often access to the same set and the number of target cache lines that can be used is much smaller. This is especially true with strides that are a big power of two (or more precisely divisible by a big power of two). The number of possible cache line that can be accesses can be computed using modular arithmetic or basic simulations. In the worst case, all accesses are done on the same cache line set (containing m cache lines). In this case, each access cause the the processor to evict one cache line in the set to load a new one in it using a replacement policy which is generally not perfect. Your Intel(R) Xeon(R) Platinum 8168 processor have the following cache properties:

  Level     Size (KiB/core)    Associativity    # Sets
-------------------------------------------------------
L1D Cache           32             8-way           64
 L2 Cache         1024            16-way         1024
 L3 Cache         1408            11-way         2048

* All cache have 64-byte cache lines

This means that is you perform accesses with a stride divisible by 4096 bytes (ie. 256 complex numbers), then all accesses will be mapped to the same L1D cache set in the L1D cache resulting in conflict misses since only 8 cache lines can be loaded simultaneously. This cause an effect called cache trashing decreasing considerably the performance. A more complete explanation is available in this post: How does the CPU cache affect the performance of a C program?.

Impact of caches on the transposition

You mentioned that block_size can be up to 256 so n1 and n3 are divisible by 256 since the provided code already make the implicit assumption that n1 and n3 are divisible by block_size and I expect n2 to be certainly divisible by 256 too. This means that the size of a line along the dimension 3 is p * 256 * (2 * 8) = 4096p bytes = 64p cache lines where p = n3 / block_size. This means that the ith item of all lines will be mapped to the exact same L1D cache set.

Since you perform a transposition between the dimension 1 and 3, this means the space between lines is even bigger. The gap between two ith items of two subsequent lines is G = 64 * p * n2 cache lines. Assuming n2 is divisible by 16, then G = 1024 * p * q cache lines where q = n2 / 16.

Having such a gap is a huge problem. Indeed, your algorithm reads/writes to many ith items of many lines in the same block. Thus, such accesses will be mapped to the same set in both the L1D and L2 caches resulting in cache trashing. If block_size > 16, cache lines will be nearly systematically reloaded to the L2 (4 times). I expect the L3 not to help much in this case since it is mostly designed for shared data between cores, its latency is quite big (50-70 cycles) and p * q is certainly divisible by a power of two. The latency cannot be mitigated by the processor due to the lack of concurrency (ie. available cache lines that could be prefetched simultaneously). This cause the bandwidth to be wasted, not to mention the non-contiguous accesses already decrease the throughput. Such an effect should already be visible with smaller power of two block_size values as shown in the previous related post (linked above).

Impact of prefetching

Intel Skylake SP processors like yours prefetch at least 2 cache lines (128 bytes) simultaneously per access in this case. This means that a block_size < 8 is not enough so to completely use prefetched cache lines of tens. As a result, a too small block_size waste the bandwidth due to prefetching and a too big also waste the bandwidth but due to cache trashing. I expect the best block_size to be close to 8.

How to address this problem

One solution is to store each block in a small temporary 2D array, then transpose it, and then write it. At first glance, it looks like it will be slower due to more memory accesses, but it is generally significantly faster. Indeed, if the block size is reasonably small (eg. <=32), then the small temporary array can completely fit in the L1 cache and is thus not subject to any cache trashing during the transposition. The block can be read as efficiently but it can be stored much more efficiently (ie. more contiguous accesses).

Adding another blocking level should help a bit to improve performance due to the L2 cache being better efficiently used (eg. with block_size set 128~256). Lebesgue curve can be used to implement a fast cache oblivious algorithm though it makes the code more complex.

Another optimization consist in adding yet another blocking level to perform an optimization called register-tiling. The idea is to use 2 nested loops operating an a tile with a small compile-time constant for the compiler to unroll the loop and generate better instructions. For example, with tile of size 4x4, this enable the compiler to generate the following code (see on Godbolt):

..B3.7:
        vmovupd   xmm0, XMMWORD PTR [rdx r8]
        vmovupd   XMMWORD PTR [r15 rdi], xmm0 
        inc       r14 
        vmovupd   xmm1, XMMWORD PTR [16 rdx r8]
        vmovupd   XMMWORD PTR [r15 r10], xmm1 
        vmovupd   xmm2, XMMWORD PTR [32 rdx r8]
        vmovupd   XMMWORD PTR [r15 r12], xmm2 
        vmovupd   xmm3, XMMWORD PTR [48 rdx r8]
        vmovupd   XMMWORD PTR [r15 r13], xmm3 
        vmovupd   xmm4, XMMWORD PTR [rdx r9]
        vmovupd   XMMWORD PTR [16 r15 rdi], xmm4 
        vmovupd   xmm5, XMMWORD PTR [16 rdx r9]
        vmovupd   XMMWORD PTR [16 r15 r10], xmm5 
        vmovupd   xmm6, XMMWORD PTR [32 rdx r9]
        vmovupd   XMMWORD PTR [16 r15 r12], xmm6 
        vmovupd   xmm7, XMMWORD PTR [48 rdx r9]
        vmovupd   XMMWORD PTR [16 r15 r13], xmm7 
        vmovupd   xmm8, XMMWORD PTR [rdx r11]
        vmovupd   XMMWORD PTR [32 r15 rdi], xmm8 
        vmovupd   xmm9, XMMWORD PTR [16 rdx r11]
        vmovupd   XMMWORD PTR [32 r15 r10], xmm9 
        vmovupd   xmm10, XMMWORD PTR [32 rdx r11]
        vmovupd   XMMWORD PTR [32 r15 r12], xmm10 
        vmovupd   xmm11, XMMWORD PTR [48 rdx r11]
        vmovupd   XMMWORD PTR [32 r15 r13], xmm11 
        vmovupd   xmm12, XMMWORD PTR [rdx rbp]
        vmovupd   XMMWORD PTR [48 r15 rdi], xmm12 
        vmovupd   xmm13, XMMWORD PTR [16 rdx rbp]
        vmovupd   XMMWORD PTR [48 r15 r10], xmm13 
        vmovupd   xmm14, XMMWORD PTR [32 rdx rbp]
        vmovupd   XMMWORD PTR [48 r15 r12], xmm14 
        vmovupd   xmm15, XMMWORD PTR [48 rdx rbp]
        vmovupd   XMMWORD PTR [48 r15 r13], xmm15 
        add       r15, rsi 
        add       rdx, 64 
        cmp       r14, rbx 
        jb        ..B3.7

Instead of this (repeated 8 times more):

..B2.12:
        vmovupd   xmm0, XMMWORD PTR [rsi r14]
        vmovupd   XMMWORD PTR [rbx r15], xmm0
        inc       rax
        vmovupd   xmm1, XMMWORD PTR [16 rsi r14]
        vmovupd   XMMWORD PTR [rbx r13], xmm1
        add       rbx, r9
        add       rsi, 32
        cmp       rax, rcx
        jb        ..B2.12

Finally, one can use AVX/AVX-2/AVX-512 intrinsics to implement a faster tile transposition for x86-64 only processors.

Note that adding some padding in the end of each line so that they are not divisible by a power of should also significantly help to reduce cache trashing. That being said, this may not be useful once the above optimizations have already been applied.