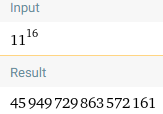
I have to compute 11^16 for a project at my Uni. Somehow Math.pow(11,16) computes a solution exactly 1 less than WolframAlpha or my other computation method.

My code is:

public class Test {
    public static void main(String args[]) {
        long a = 11;
        long b = 16;
        System.out.println(""   (long)Math.pow(a, b));
        System.out.println(""   squareAndMultiply(a, b));
    }

    public static long squareAndMultiply(long b, long e){
        long result = 1;
        long sq = b;
        while(e>0){
            if(e%2==1){
                result *= sq;
            }
            sq = sq * sq;
            e /= 2;
        }
        return result;
    }
}

The result from the code is:

math.pow(11,16):

45949729863572160

squareAndMultiply(11,16):

45949729863572161

CodePudding user response：

With floating-point arithmetic, you're in that gray zone where the precision of a double is less than that of a long (even if the range of a double is much bigger).

A double has 53 bits of precision, whereas a long can devote all 64 bits to precision. When you're dealing with values as high as 11¹⁶, the difference between one double value and the next one up becomes noticeable.

Java has a built-in method Math.ulp ("unit in last place") that effectively gives the difference in values between consecutive representable values. (There's a double version and a float version.)

System.out.println(Math.ulp(Math.pow(11, 16)));

8.0

That means the least possible double value greater than 45949729863572160 is 45949729863572168.

The long value 45949729863572161 is correct, but the value you're getting with Math.pow, 45949729863572160, is as close as a double can get to the true answer, given its limited (but still large) precision.

Casting to a long makes no difference, because Math.pow already computes the result as a double, so the answer is off by one already. Your long method of computing the value is correct.

If you're computing values that would overflow long, then instead of using double, you can use BigDecimal, which has its own pow method to retain a precision of 1.0.

CodePudding user response：

The root cause of this discrepancy is loss of precision because of Double precision numbers are accurate up to sixteen decimal places.

One way to demonstrate is this example.

System.out.println((double)999999999999999999L);

outputs:

1.0E18

The output of Math.pow(11, 16) is 4.594972986357216E16, which on casting to long gets converted into 45949729863572160.

If you are interested more in learning about the loss of precision, you can check this.