The problem is: Given this kind of forest:

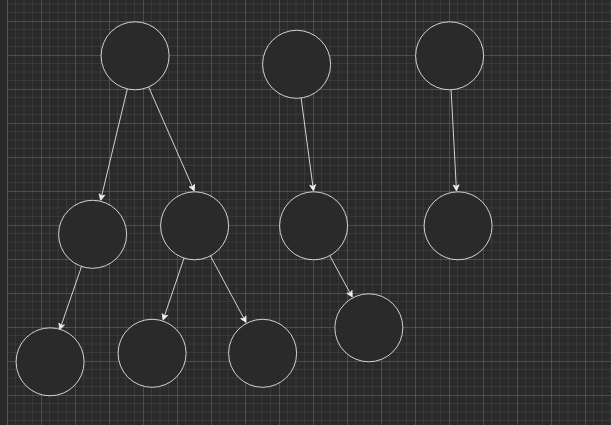if we have a node, how can we get the descendants of it?

I thought this algorithm that I think is pretty efficient when talking about reading all descendants adding some little overhead in the writing(it's not too much):

Firstly, to simplify, let's suppose that the number of root nodes is limited to N. We then will need to store a list with the N first primes. When we create the first node we will assign the 2nd prime of our list (3) to a field name treeId, the second root node gets the 3rd prime, and so on (we can keep a counter of how many roots there are).

To create a child of a parent, we will take the parent's treeId and recursively multiply to the parent of parent treeId and then multiply by 2 (the first prime). To know all descendent of a node with nodeId = k, we can do a linear search and get all nodes whose treeId is different than k and is divisible by k.

We can remove the limit of N records as root creating another index treeGroupId so that a child will inherit the same treeGroupId of the parent and we verify if two nodes have the same treeGroupId to then apply the first verification algorithm.

My question is: Is this a known technique to search for Tree decendents? Is there any flow in this algorithm. If there's can we have better result?

CodePudding user response：

In the context of prime factorization, one known solution strategy is to use a so-called factor tree.