I have a question about the leetcode graph problem [133. Clone Graph] "https://leetcode.com/problems/clone-graph/".

I used DFS to solve this problem and here is my code by javascript:

/**
 * // Definition for a Node.
 * function Node(val, neighbors) {
 *    this.val = val === undefined ? 0 : val;
 *    this.neighbors = neighbors === undefined ? [] : neighbors;
 * };
 */

/**
 * @param {Node} node
 * @return {Node}
 */
var cloneGraph = function(node) {
    if(!node) return null;
    const visited = new Map();
    
    const dfs = (node) => {
        const n = [];
        if(visited.has(node.val)) return visited.get(node.val);
        let newNode = new Node(node.val);
        visited.set(node.val,newNode);
        
        for(let on of node.neighbors){
            n.push(dfs(on));
        }
        
        newNode.neighbors = n;
        return newNode;
    }
    
    return dfs(node);
};

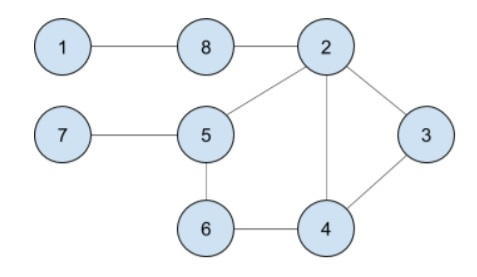
My solution graph would be like this:

Assumed that V/E is the Vertexes/Edges of the Graph.

I figured out that there're lots of people said the time complexity of this problem is O(V E), but I can't catch it because I think it's O(E) in this case.

In my opinion, our input is only a node object instead of an adjacent list and it's an undirected graph, so we don't need to check a consecutive sequence for each node, we just need to trace it from the input "node" and then it would scan the whole graph, that's only a kind of normal DFS like trees problem.

Is it anything wrong there? If it is, Could anyone please explain why I got a misunderstanding of this solution?

CodePudding user response：

I figured out that there're lots of people said the time complexity of this problem is O(V E), but I can't catch it because I think it's O(E) in this case.

You are absolutely right. The code challenge says that the graph is connected and this is an important information. That means that there are at least V - 1 edges. Since the algorithm is driven by visiting edges only once in each direction, and nodes are not visited in another way than by traveling over an edge (except once, for the first node), O(E) is the same as O(V E).

CodePudding user response：

In every simple graph with n vertices, the number of edges is bound by n^2, so O(E) = O(V^2). This bound is tight as can be seen with the complete graphs (every vertex connects to each other).

However, for many (natural or contrived) classes of graphs there are restrictions on the number of edges known beforehand (eg. trees have exactly V-1 edges), therefore it is popular to express complexity measures depending on V and E being formally treated as independent entities.

In general, DFS involves O(V E) operations since ...

1. Every vertex is visited, be it as the initial vertex in a new component for disconnected graphs, be it in the course of following edges during the dfs proper.
2. (Close to) Every edge is visited: you could only skip one if you knew beforehand that it ends at a vertex already seen, but to know that you need to follow the edge to find out ...

There seems to be a possible shortcut: stop the dfs as soon as you've seen all vertices. But that depends on the purpose of the dfs - if you want to build a spanning tree, it is ok, if you want to detect a cycle it is not.

Back to your specific setting: Trivially all vertices and all edges must be visited to clone a graph, thus O(V E). However, if the graph is connected, you know beforehand that you'll have seen all vertices after having visited all edges, thus: O(E).