How to generate a negative exponential distribution in R-CodePudding

I was manually creating a negative exponent distribution today and was trying to figure out a faster/easier solution. First, I just manually crafted a geometric sequence such as this one, multiplying constantly by .60 til I neared zero:

x <- 400
x*.60

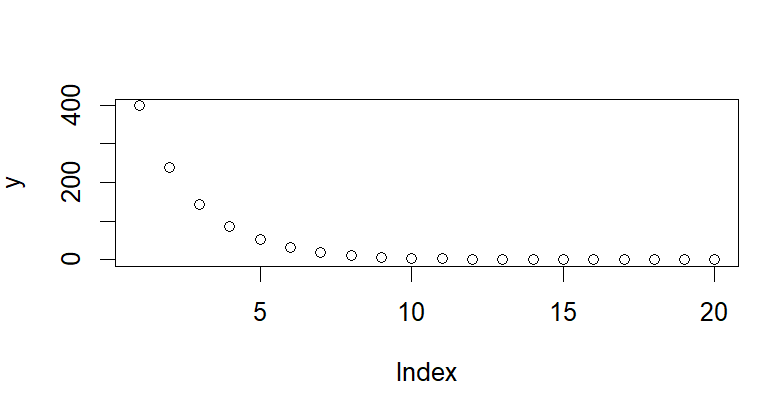
Doing this about 20 times, I got this vector of solutions and plotted the distribution, as seen below:

y <- c(400,240,144,86.4, 51.84, 31.104, 18.6624, 11.19744, 6.718464, 4.031078,
       2.418647, 1.451188, .8707129, .5224278, .3134567, .188074, .1128444,
       .06770664, .04062398, .02437439)
plot(y)

However, I was trying to figure out what must be an easier way of doing this with seq, but I only know how to do this with arithmetic sequences. I tried reproducing what I did below:

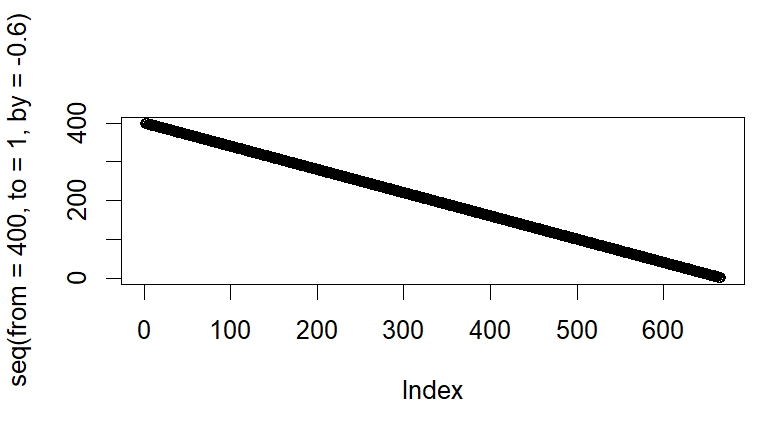
plot(seq(from=400,
    to=1,
    by=-.60))

Which obviously doesn't produce the same effect, causing a very linear decline when plotted:

Is there an easier solution? I have to imagine that this is a rather basic function within R.

CodePudding user response：

You may use dexp.

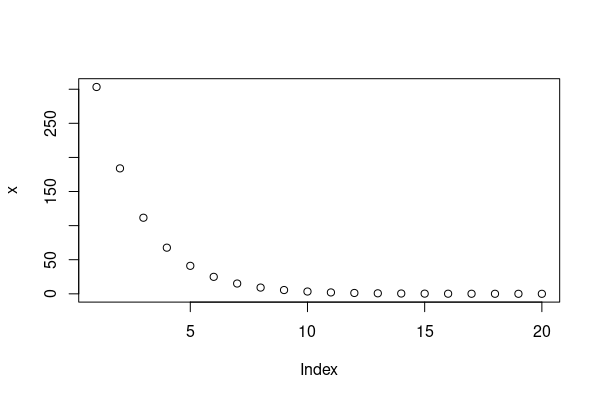
(x <- dexp(1:20, rate=.5)*1000)
# [1] 303.26532986 183.93972059 111.56508007  67.66764162  41.04249931  24.89353418  15.09869171   9.15781944   5.55449827
# [10]   3.36897350   2.04338572   1.23937609   0.75171960   0.45594098   0.27654219   0.16773131   0.10173418   0.06170490
# [19]   0.03742591   0.02269996

plot(x)

To make it start exactly at 400, we can minimize (400 - dexp(1, rate=.5)*x)^2 using optimize.

f <- function(x, a) (a - dexp(1, rate=.5)*x)^2
xmin <- optimize(f, c(0, 4000), a=400)

(x <- dexp(seq_len(20), rate=.5)*xmin$minimum)
# [1] 400.00000000 242.61226389 147.15177647  89.25206406  54.13411329  32.83399945  19.91482735  12.07895337   7.32625556
# [10]   4.44359862   2.69517880   1.63470858   0.99150087   0.60137568   0.36475279   0.22123375   0.13418505   0.08138735
# [19]   0.04936392   0.02994073

Note that if you want any different rate= you should to use it both in optimize and when creating the values.