Find the size/level of a node from its position within an quadtree-CodePudding

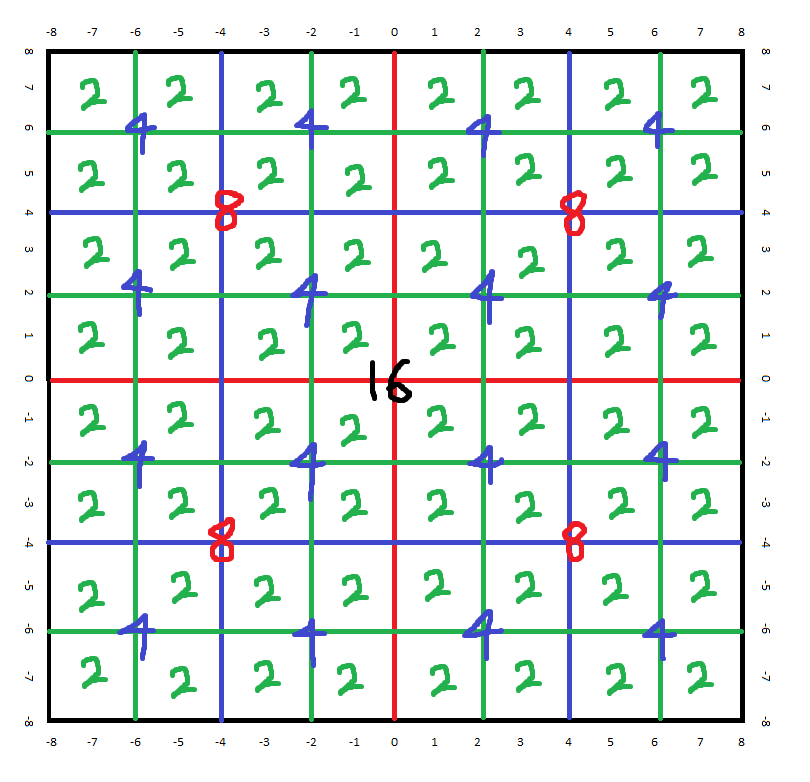
I have a quadtree. The root node (level 0) is positioned at 0,0 by its centre. It has a width of 16, so its corners are at -8,-8 and 8,8. Since it's a quadtree, the root contains four children, each of which contain four children of their own and so on. The deepest level is level 3 at width 2. Here's a dodgy Paint drawing to better illustrate what I mean:

The large numbers indicate the centre position and width of each node. The small numbers around the sides indicate positions.

Given a valid position, how can I figure out what level or size of node exists at that position? It seems like this should be obvious but I can't get my head around the maths. I see the patterns in the diagram but I can't seem to translate it into code.

For instance, the node at position 1,1 is size 2/level 3. Position 4,6 is invalid because it's between nodes. Position -6,-2 is size 4/level 2.

Additional Notes:

Positions are addresses. They are exact and not worldspace, which is why it's possible to have an invalid address.
In practice the root node size could be as large as 4096, or even larger.

CodePudding user response：

Observe that the coordinate values for the centre of each node are always /- odd multiples of a power-of-2, the latter being related to the node size:

Node size | Allowed centre coordinates | Factor
-----------------------------------------------------
    2     | 1, 3, 5, 7, 9, 11 ...      | 1 = 2/2
-----------------------------------------------------
    4     | 2, 6, 10, 14, 18, 22 ...   | 2 = 4/2
-----------------------------------------------------
    8     | 4, 12, 20, 28, 36, 44 ...  | 4 = 8/2
-----------------------------------------------------
    16    | 8, 24, 40, 56, 72, 88 ...  | 8 = 16/2

The root node is a special case since it is always centred on 0,0, but in a larger quad-tree the 16x16 nodes would follow the same pattern.

Crucially, both X,Y values of the coordinate must share the same power-of-2 factor. This means that the binary representations of their absolute values must have the same number of trailing zeros. For your examples:

Example | Binary | Zeros | Valid
----------------------------------
  X = 1 | 000001 |     0 |   Y
  Y = 1 | 000001 |     0 | S = 2
----------------------------------
  X = 4 | 000100 |     2 |   N
  Y = 6 | 000110 |     1 |
----------------------------------
  X =-6 | 000110 |     1 |   Y
  Y =-2 | 000010 |     1 | S = 4

Expressions for the desired results:

Size (S) = 2 ^ (Zeros 1)
Level = [Maximum Level] - Zeros