My goal is to calculate the slope of a curve.
I read that I can take the first derivation for this. Which in turn requires a formula that describes my data. So I am looking into curve fits rigth now, but can not find anything that describes how to fit curves properly with date objects in them.
My data are measurements taken at irregular time intervals, and is just incrementing at different rates, but lets ignore this for now, as it makes stuff even more complicated and I am looking for the basics. The data can be represented by the economics dataset from ggplot:
library(ggplot2)
ggplot(economics, aes(date, pce))
geom_area()
Main question How to take the first derivation of a curve fit containing date objects? Can I just convert them to a numeric, and will this distort the result?
Fitting a linear model works, but for fit2, I will get an error.
fit1 <- lm(pce ~ date, data = economics)
fit2 <- lm(pce ~ poly(date, 2, raw = T), data = economics)
Error in Ops.Date(X, Y, ...) : ^ not defined for "Date" objects
Side question
Note that I am looking for things like weekly variations. So I need a fit that is very detailed.
geom_smooth can effortlessly fit a function to my data even if x-axis is still in date format, but the loess curve or lm that I have seen with this will not do the trick for me, as they hide the interesting aspects.
So maybe I am in the wrong place and should use element wise differentation? And if yes, how does it work?
Thank you for helping or giving me resources where I can find the solutions.
CodePudding user response:
You can use the stat_smooth function where you can use the method "lm" with your own formula like this:
library(ggplot2)
ggplot(economics, aes(date, pce))
stat_smooth(method = "lm", formula = y ~ poly(x, 2, raw = TRUE), size = 1)
geom_area(alpha = 0.3)
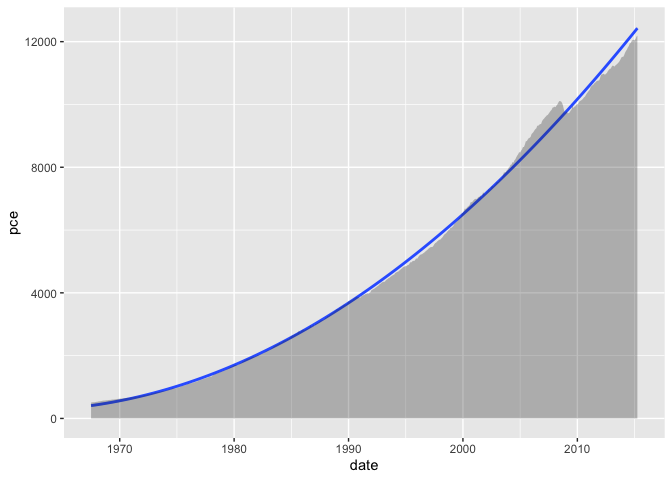
Created on 2022-07-22 by the reprex package (v2.0.1)
CodePudding user response:
If you look at the documentation for the Dates class, you'll see that it's actually the number of days since January 1, 1970:
Dates are represented as the number of days since 1970-01-01, with negative values for earlier dates. They are always printed following the rules of the current Gregorian calendar, even though that calendar was not in use long ago (it was adopted in 1752 in Great Britain and its colonies). It is intended that the date should be an integer, but this is not enforced in the internal representation.
Accordingly, you can convert to numeric and include it as a predictor with no issue:
library(ggplot2)
# Date class is just a numeric value
economics$date_num <- as.numeric(economics$date)
economics$date_num[1:40]
#> [1] -915 -884 -853 -823 -792 -762 -731 -700 -671 -640 -610 -579 -549 -518 -487
#> [16] -457 -426 -396 -365 -334 -306 -275 -245 -214 -184 -153 -122 -92 -61 -31
#> [31] 0 31 59 90 120 151 181 212 243 273
# Fit linear model
lm(pce ~ poly(date_num, 2, raw = T), data = economics)
#>
#> Call:
#> lm(formula = pce ~ poly(date_num, 2, raw = T), data = economics)
#>
#> Coefficients:
#> (Intercept) poly(date_num, 2, raw = T)1
#> 5.614e 02 1.960e-01
#> poly(date_num, 2, raw = T)2
#> 3.159e-05
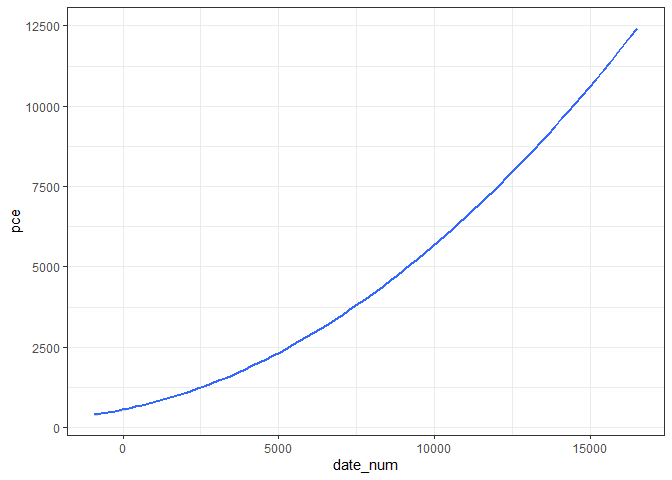
We can also include the model directly in ggplot using the formula argument in stat_smooth:
# Plot with quadratic term
ggplot(economics, aes(date_num, pce))
stat_smooth(method = "lm",
formula = y ~ poly(x, 2, raw = TRUE))
theme_bw()
You can also just use lm() to fit a model. A nice feature of this is that you can specify the dates for which you want slope of the curve, although note that your model is just extrapolating for dates outside of the observed data.
# Fit model
mod <- lm(data = economics, pce ~ poly(date_num,2,raw = T))
# Generate dates for which you want to calculate derivative
new_data <- data.frame(date_num = -200:200)
# Get predictions for each date, add to data
new_data$pce_pred <- predict(mod,newdata = data.frame(date_num = -200:200))
# Compute derivatives at midpoint, add to data
# NOTE: need to add NA since first is empty
new_data$slope <- c(NA, with(new_data, diff(pce_pred) / diff(date_num)))