I try to get this code developed for a potential project at work and I think Dijkstra can help but no idea how to get started.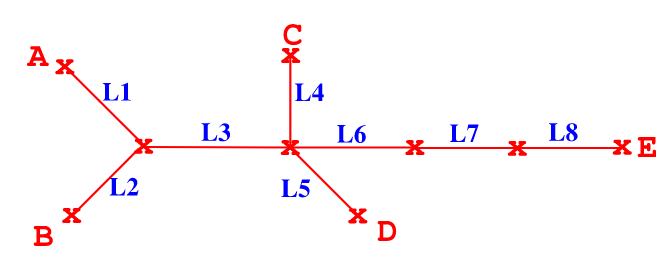

I have a list of Line objects called myList and each line has EndPoint1 and EndPoint2 as Point2Dcordinates (x,y) and Name as string. So the list has L1, L2, L3, L4, L5, L6, L7, and L8 as shown in the example image. Points A, B, C, D, and E are points of these lines and they are always not connected points between two lines.

I would like to write a method that gives me a list of the lines (or names of the lines) that connected two points for example:

List<string> FindPath(Point2D P1, Point2D P2): (A, E): L1, L3, L6, L7, L8
List<string> FindPath(Point2D P1, Point2D P2): (B, D): L2, L3, L5

Edit:I would like to find all possible paths, although 99.9% of the time there is only 1 path possible.

CodePudding user response：

You can solve this by treating it as a graph. Each x is a vertex, and your lines are the edges. Then to find the path between P1 and P2, run BFS from P1.

CodePudding user response：

I am assuming you need to find the shortest path from one point to another. Hence you need to do a BFS. First convert the points into a graph. The graph could be of the format

// The key is the point and the it contains the list of all 
// the neighbours
Map<Point2D, List<Point2D>> graph = new HashMap<>();

Then use a Queue and a visited matrix to keep track of the visited points. When looping through the Points make sure you add them to an answer list. For more details on BFS look here: https://www.geeksforgeeks.org/print-paths-given-source-destination-using-bfs/

CodePudding user response：

You are talking about a data structure called a graph, a collection of nodes (points), connected by edges (line segments).

Graphs comes in several flavours. They can be directed or undirected, and they can by cyclic, or acyclic.

Directed graphs have one-way edges: the edge a→b can only be used to travel from a to b, it can't be used to get from b to a. Undirected graphs, on the other hand, have 2-way edges: as long as two nodes are connected, you can get from either one to the other.

Cyclic graphs allow cycles, where traversing the graph can return you to a node you have already visited (a → b → c → a is a cycle); acyclic graphs do not allow such cycles. If your graph is cyclic, when you traverse it, you'll need to track what nodes you've visited, so you can detect and deal with cycles. If you don't you'll wind up in an endless loop.

In addition, both nodes and edges may carry additional information, such as "cost", making them a weighted graph. Google's and Apple's maps are modeled as such weighted graphs. Each intersection is a node, and each street segment between intersections is an edge. The additional information (weigths) carried by edges are information such as average speed, starting/ending addresses, etc.

If you need to find the shortest path between two nodes in your graph, you may need a weighted graph (where the edges carry a distance. Or not: perhaps "shortest path" is defined as the least number of intermediate nodes between A and B.

So, you need the correct model:

• a set of nodes, and
• a set of edges, defined by the 2 nodes it connects.

One can (and it is sometimes useful to dispense with the set of nodes completely, and define the graph solely in terms of its edges:

Once you have that, finding a path from any two points in the graph is actually pretty easy. The algorithm is this:

• You can get from node A to node B if an edge AB exists. Otherwise...
• You can get from node A to node B if
  • an edge AX exists, and
  • you have not yet visited node X, and
  • you can [recursively] get from node X to node B.

That's about all there is to it.