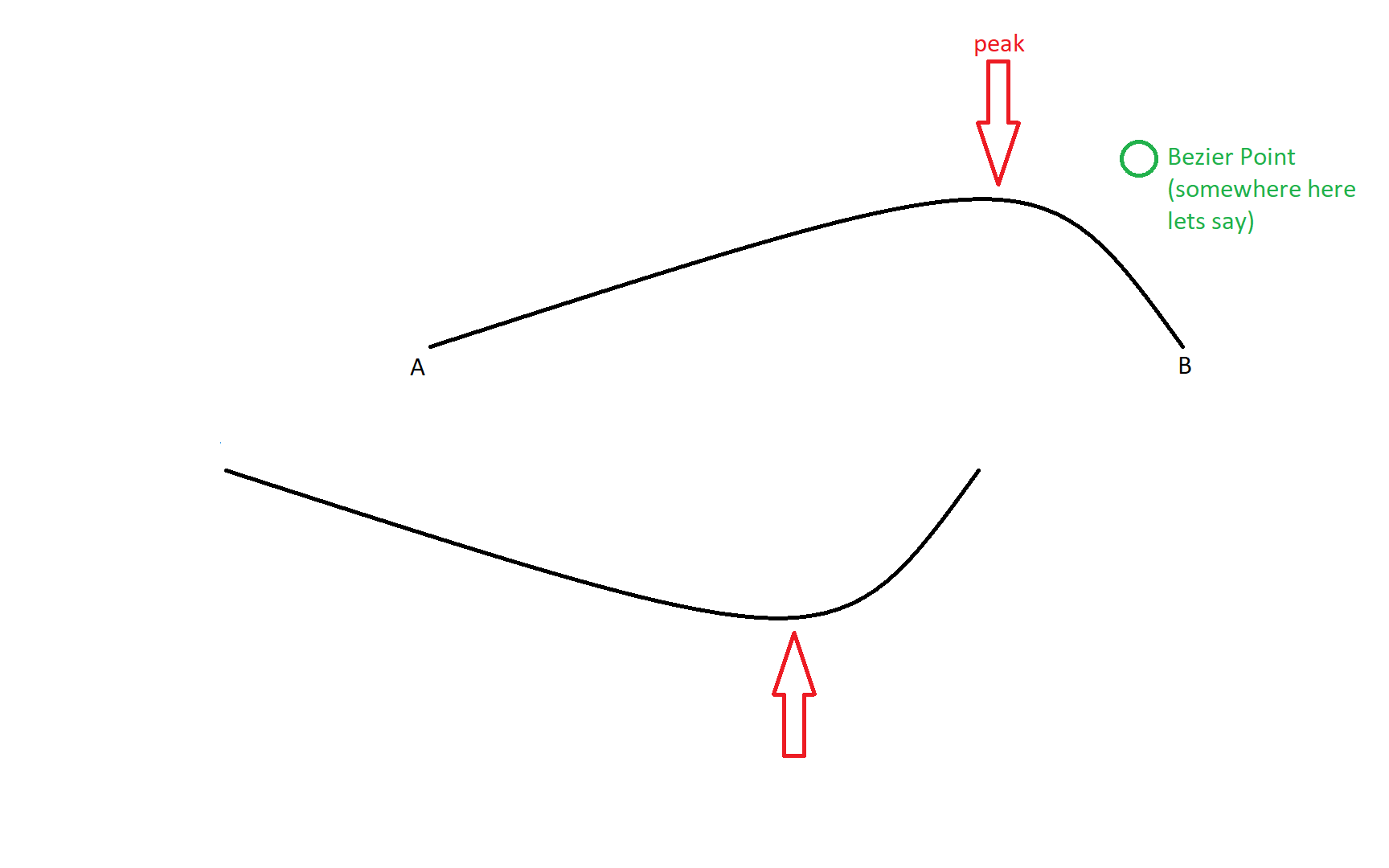
I am creating an svg arc between two points. I am interested in creating a slightly curved arc and adding an svg circle element at the peak of the arc (i.e. where the curve changes orientation).
Based on some basic search, creating this curve is possible using a quadratic bezier arc which I give it the start point, bezier point, and end point (ex. M20 50 Q50 10, 100 80). Obviously my values will be dynamic so in order to determine where to position my circle (cx, cy) I want to know where the curve reaches its maximum because this is not the same as the bezier point.
Is there a way to know the coordinates of such point? I am quite new to svg so if there's a better way in the first place (other than quadratic bezier?) that'd also work.
Thanks!
CodePudding user response:
Note that you're not looking for the point where the orientation of the curve" changes, because orientation is a well defined concept in maths and means the way in which we travel along a curve. For instance, the Bezier curves p1,p2,p3 and p3,p2,p1 look identical, but have opposite orientation.
What you're looking for is an extremum in a coordinate system that is "aligned" with the curve. Unfortunately, there is no single such coordinate system, so you have to pick one, but we can pick one that looks reasonable enough: we can find "the" point by realigning the curve to the x-axis, then find the point where the y derivative is zero. As the derivative for a quadratic curve is a straight line, we can almost trivially find this y value.
const { cos, sin, atan2 } = Math;
function map(v, s1,e1, s2,e2) {
return s2 (v-s1) * (e2-s2)/(e1-s1);
}
const path = original.getAttribute(`d`);
const terms = path.replace(/[A-Z]/g, ``).split(/\s /).map(v => parseFloat(v));
const points = [];
for(let i=0, e=terms.length; i<e; i=i 2) points[i/2] = terms.slice(i,i 2);
// Let's do the thing, which we don't actually need to do because for
// quadratic curves it'll turn out we already know at which "t" value
// the axis-aligned extremum can be found. But let's discover that anyway:
(function findExtremum([p1, p2, p3]) {
const [sx, sy] = p1;
const [cx, cy] = p2;
const [ex, ey] = p3;
// In order to realign, we only need to recompute three points.
// The other three are all zero.
const a = atan2(ey-sy, ex-sx);
const newcx = (cx-sx) * cos(-a) - (cy-sy) * sin(-a);
const newcy = (cx-sx) * sin(-a) (cy-sy) * cos(-a);
const newex = (ex-sx) * cos(-a) - (ey-sy) * sin(-a);
aligned.setAttribute(`d`, `M0 0 Q${newcx} ${newcy} ${newex} 0`);
// If we work out the derivative, we discover we don't need it
// thanks to our translation/rotation"
const d = [
[2 * (newcx - 0), 2 * (newcy - 0)],
[2 * (newex - newcx), 2 * (0 - newcy)],
];
// we see two y values that are the same, except for the sign,
// and so the zero crossing lies at the midpoint, i.e. at the
// bezier control value t=0.5, and with that knowledge we can
// find the original point:
const t = 0.5;
// This is all we needed, and all the code we've written so far
// turns out to have been irrelevant: for quadratic curves, the
// axis-aligned extremum is *always* at t=0.5, so let's just plug
// that into our curves to see the result:
const x = 2 * newcx * (1-t) * t newex * t**2;
const y = 2 * newcy * (1-t) * t;
extremum.setAttribute(`cx`, x);
extremum.setAttribute(`cy`, y);
// and for our original curve:
const ox = sx * (1-t)**2 2 * cx * (1-t) * t ex * t**2;
const oy = sy * (1-t)**2 2 * cy * (1-t) * t ey * t**2;
point.setAttribute(`cx`, ox);
point.setAttribute(`cy`, oy);
})(points);svg { border: 1px solid grey; }
p { display: inline-block; height: 120px; vertical-align: 40px; }<svg width="120" height="100" viewBox="0 0 120 100">
<path id="original" fill="none" stroke="black" d="M20 50 Q50 10 100 80"/>
</svg>
<p>→</p>
<svg width="120" height="100" viewBox="0 0 120 100">
<g transform="translate(20,80)">
<path fill="none" stroke="grey" d="M0 -100L0 200M-100 0L200 0"/>
<path id="aligned" fill="none" stroke="black" d=""/>
<circle id="extremum" cx="0" cy="0" r="2"/>
</g>
</svg>
<p>→</p>
<svg width="120" height="100" viewBox="0 0 120 100">
<path fill="none" stroke="black" d="M20 50 Q50 10 100 80"/>
<circle id="point" cx="0" cy="0" r="2"/>
</svg>In fact, we can find it so trivially that, if you read through the code, we don't even need this code. The extremum's going to be at t=0.5, which is where the control point has the most influence of the curve, and the radius of curvature is the smallest. We can bypass literally everything we just did (now that we've determined we don't need it) and just directly calculate what we need:
const path = original.getAttribute(`d`);
const terms = path.replace(/[A-Z]/g, ``).split(/\s /).map(v => parseFloat(v));
const points = [];
for(let i=0, e=terms.length; i<e; i=i 2) points[i/2] = terms.slice(i,i 2);
// If t-0.5 then (1-t)^2, (1-t)t, and t^2 are all 0.25, so
// we can, again, drastically simplify the actual calculation:
const x = (points[0][0] 2*points[1][0] points[2][0])/4;
const y = (points[0][1] 2*points[1][1] points[2][1])/4;
point.setAttribute(`cx`, x);
point.setAttribute(`cy`, y);svg { border: 1px solid grey; }
p { display: inline-block; height: 120px; vertical-align: 40px; }<svg width="120" height="100" viewBox="0 0 120 100">
<path id="original" fill="none" stroke="black" d="M20 50 Q50 10 100 80"/>
</svg>
<p>→</p>
<svg width="120" height="100" viewBox="0 0 120 100">
<path fill="none" stroke="black" d="M20 50 Q50 10 100 80"/>
<circle id="point" cx="0" cy="0" r="2"/>
</svg>Done.
CodePudding user response:
Brute force:
- get the total length of the path
- check y value for each point on the path
For multiple paths in one SVG:
Note the logic error for the pink path you have to fix
<peak-point>
<svg>
<path d="M20 50 Q50 10, 100 80"/>
<path d="M 10 49 Q 13 111 74 97" fill="pink"/>
</svg>
</peak-point>
<script>
customElements.define('peak-point', class extends HTMLElement {
connectedCallback() {
setTimeout(() => { // make sure innerHTML SVG is parsed
this.querySelectorAll("path").forEach(path => {
const len = path.getTotalLength();
let point;
let pos = 0;
let pointAt = (at) => (point = path.getPointAtLength(at));
let previous_y = pointAt(0).y;
while (previous_y >= pointAt(pos).y) {
previous_y = point.y;
pos ;
}
path.insertAdjacentHTML("afterend",
`<circle cx="${point.x}" cy="${point.y}" r=5 fill="red"/>`);
})
})
}
});
</script>