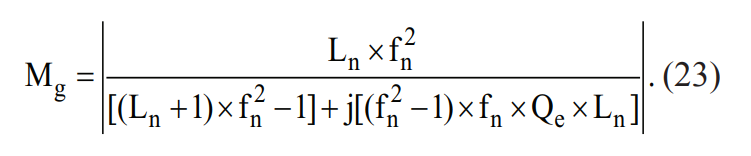Numpy: Complex Equation Curve is Plotted Incorrectly-CodePudding

I am trying to use the Python to do some graphical analysis.

I need to plot this equation: Where fn is on the x axis (log scale 0 - 10) and Mg is on the y axis. Ln and Qe are dummy variables that I will enter different values for, but for now I am working with just

Ln = 5
Qe = 0.5

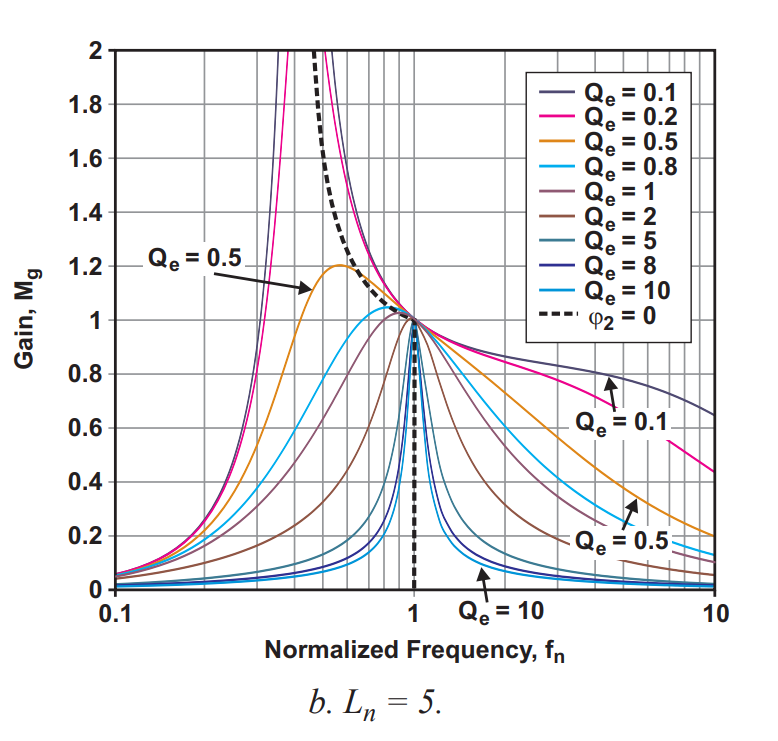
The plot is supposed to look something like this:

Mind you I am only trying to plot one value for Qe at this time, so we would only see one curve.

Here is the code I have so far:

    import numpy as np
    import pylab
    import matplotlib.pyplot as plt
    import math
    Ln = 5
    Qe = .5
    fn = np.linspace(.1, 10, 1000)
    Mg_Num = Ln * fn**2
    Mg_Dem = ((Ln   1) * (fn**2 - 1))   ((fn**2 - 1) * fn * Qe * Ln)
    Mg = abs(Mg_Num/Mg_Dem)
    
    plt.plot(fn, Mg)
    plt.xscale('log')
    
    plt.show()

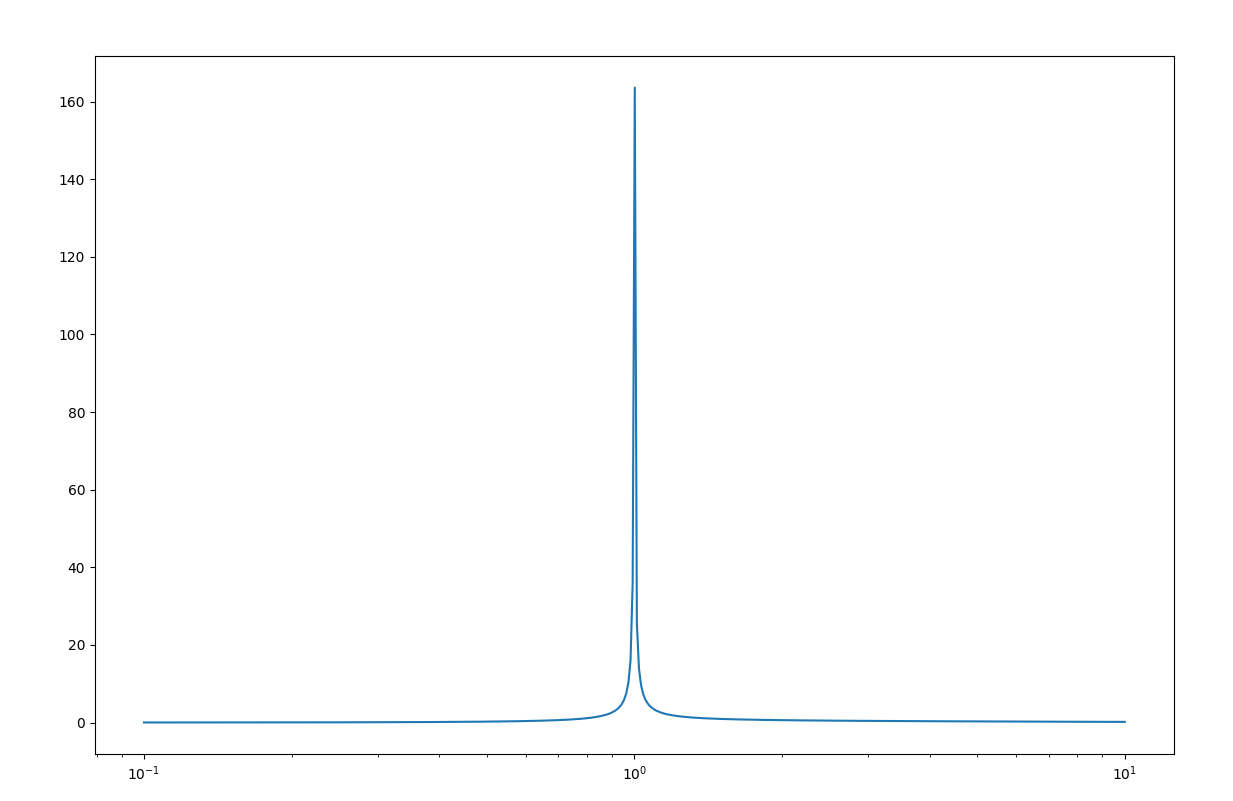
And this is the plot it generates:

It does not really look like the curve of Ln = 5, Qe = 0.5 (orange curve) in the graph above.

I am thinking maybe it has to do with the imaginary part of Mg in the denominator, but I am not sure how to incorporate that into such a complex equation (no pun intended).

Any suggestions on what I should do?

CodePudding user response：

You can write complex functions by using j. For example x = 3 5j. Besides the imaginary part you had a placed a parenthesis incorrectly.

import numpy as np
import matplotlib.pyplot as plt

Ln = 5
Qe = .5
fn = np.linspace(.1, 10, 1000)

Mg_Num = Ln * fn**2
Mg_Dem = ((Ln   1) *  fn**2 - 1 )   1j*((fn**2 - 1) * fn * Qe * Ln)
#                    ^         ^    ^^ 
Mg = np.abs(Mg_Num / Mg_Dem)

plt.plot(fn, Mg)
plt.xscale('log')
plt.show()