I am currently working on a project in MATLAB that compares two different numerical methods (direct and iterative), each for two different matrix sizes, to the actual analytic solution of the system. The first .m file included below provides an implementation of a tridiagonal matrix solver, where the main function plots a solution for two different sizes of tridiagonal matrices: a 2500x2500 matrix and 50x50 matrix.

function main
n=50; 
for i=1:2
di=2*ones(n,1);
up=-ones(n,1);
lo=-ones(n,1);
b=ones(n,1)/(n*n); 
[subl,du,supu]=tridiag_factor(lo,di,up);
usol = tridiag_solve(subl,du,supu,b);
%figure(i)
plot(usol);
hold on;
title(['tridiag ' num2str(n) '']) 
n=2500; 
end


function [subl,du,supu]=tridiag_factor(subd,d,supd)
n=length(d);
for i=1:n-1
subd(i)=subd(i)/d(i);
d(i 1)=d(i 1)-subd(i)*supd(i);
end
subl=subd; supu=supd; du=d;

function x = tridiag_solve(subl,du,supu,b)

% forward solve
n=length(b); z=b; 
z(1)=b(1);
for i=2:n
z(i)=b(i)-subl(i)*z(i-1);
end
% back solve
x(n)=z(n);
for i=n-1:-1:1
x(i)=(z(i)-supu(i)*x(i 1))/du(i);
end

I have included a hold on statement after the first usol is plotted so I can capture the second usol on the same figure during the second iteration of the for loop. The next piece of code is a Jacobi method that iteratively solves a system for a tridiagonal matrix. In my case, I have constructed two tridiagonal matrices of different sizes which I will provide after this piece of code:

function [xf,r] = jacobi(A,b,x,tol,K)
%
%  The function jacobi applies Jacobi's method to solve A*x = b.
%  On entry:
%    A       coefficient matrix of the linear system;
%    b       right-hand side vector of the linear system;
%    x       initial approximation;
%    eps     accuracy requirement: sx=top when norm(dx) < eps;
%    K       maximal number of steps allowed.
%  On return:
%    x       approximation for the solution of A*x = b;
%    r       residual vector last used to update x,
%            if success, then norm(r) < eps.[
%
n = size(A,1);
fprintf('Running the method of Jacobi...\n');
for k = 1:K
      % r = b - A*x;
    for i=1:n
        sum=0;
        for j = 1:n
            if j~=i
                sum=sum A(i,j)*x(j);
            end
        end
        x(i)=(b(i)-sum)/(A(i,i));
    end;
    k=k 1;
    r = b - A*x;
%     fprintf('  norm(r) = %.4e\n', norm(r));
    if (norm(r) < tol)
        fprintf('Succeeded in %d steps\n', k);
        return;
    end;
end
fprintf('Failed to reached accuracy requirement in %d steps.\n', K);
xf=x;

%r(j) = r(j)/A(j,j);
%x(j) = x(j)   r(j);

Now, lastly, here is my code for the two tridiagonal matrices (and other related information for each system corresponding to the appropriate matrices) I wish to use in my two jacobi function calls:

% First tridiagonal matrix 
n=50; 
A_50=full(gallery('tridiag', n, -1, 2, -1));

% Second tridiagonal matrix 
n=2500; 
A_2500=full(gallery('tridiag', n, -1, 2, -1));

K=10000;
tol=1e-6;

b_A50=ones(length(A_50), 1);
for i=1:length(A_50)
    b_A50(i,1)=0.0004;
end 
x_A50=ones(length(A_50),1);


b_A2500=ones(length(A_2500), 1);
for i=1:length(A_2500)
    b_A2500(i,1)= 1.6e-7;
end 
x_A25000=ones(length(A_2500),1);

As stated in the question header, I need to plot the vectors produced from jacobi(A_50,b_A50,x_A50,tol,K), jacobi(A_2500,b_A2500,x_A25000,tol,K) and a mathematical function y=@(x) -0.5*(x-1)*x all on the same figure along with the two usol (for n=50 and n=2500) produced by the main function shown in the first piece of code, but I have had no luck due to the different lengths of vectors. I understand this is probably an easy fix, but of course my novice MATLAB skills are not sufficing.

Note: I understand x_A50 and x_A2500 are trivial choices for x, but I figured while I ask for help I better keep it simple for now and not create any more issues in my code.

CodePudding user response：

1. In MATLAB traces sent to same plot must have same length.

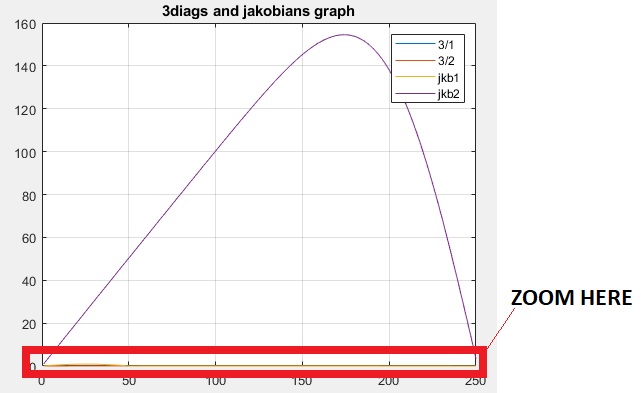
2. I have allocated just one variable containing all traces, for the respective tridiagonals and resulting traces out of your jacobi function.

3. I have shortened from 2500 to 250, and the reason is that with 2500, compared to 50, the tridiag traces, and the short jacobi are so flat compared to the last trace than one has to recur to dB scale to find them on same graph window as you asked.

4. 1st generate all data, and then plot all data.

So here you have the script plotting all traces in same graph :

clear all;close all;clc

n=[50 250]; 

us_ol=zeros(numel(n),max(n));

% generate data
for k=[1:1:numel(n)]
    di=2*ones(n(k),1);
    up=-ones(n(k),1);
    lo=-ones(n(k),1);
    b=ones(n(k),1)/(n(k)*n(k)); 
    [subl,du,supu]=tridiag_factor(lo,di,up);
    us_ol0 = tridiag_solve(subl,du,supu,b);
    us_ol(k,[1:numel(us_ol0)])=us_ol0;
end 

n_us_ol=[1:1:size(us_ol,2)];

str1=['tridiag ' num2str(n(1))];
str2=['tridiag ' num2str(n(2))];
legend(str1,str2);
grid on

% the jacobi traces

nstp=1e3;
tol=1e-6;

A1=zeros(max(n),max(n),numel(n));

for k=1:1:numel(n)
    A0=full(gallery('tridiag', n(k), -1, 2, -1));
    A1([1:1:size(A0,1)],[1:1:size(A0,2)],k)=A0;
end

b_A1=ones(max(n),max(n),numel(n));

for k=1:1:numel(n)

for i=1:n(k)
    b_A1(i,1,k)=0.0004;
end 

end
 
n_A1=[1:1:size(A1,1)];

jkb=zeros(numel(n),max(n));

for k=1:1:numel(n)
    A0=A1([1:n(k)],[1:n(k)],k);
    b_A0=b_A1([1:n(k)],[1:n(k)],k);
    n0=[1:1:n(k)];
    jkb0=jacobi(A0,b_A0,n0',tol,nstp)
    jkb(k,[1:numel(jkb0)])=jkb0';
end

% plot data
figure(1)
ax1=gca
plot(ax1,n_us_ol,us_ol(1,:),n_us_ol,us_ol(2,:));
hold(ax1,'on')
plot(ax1,n_A1,jkb(1,:),n_A1,jkb(2,:))

grid on
legend('3/1','3/2','jkb1','jkb2')
title('3diags and jakobians graph')

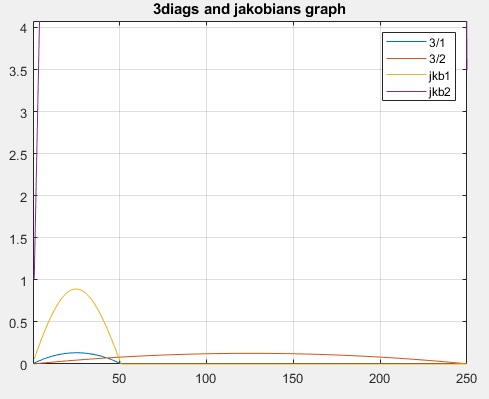
As mentioned above, one has to zoom to find some of the traces

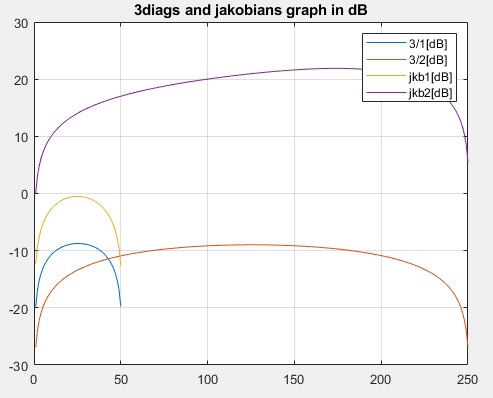
One way to combine really small traces with large traces is to use Y log scale

figure(2)
ax2=gca
plot(ax2,n_us_ol,10*log10(us_ol(1,:)),n_us_ol,10*log10(us_ol(2,:)));
hold(ax2,'on')
plot(ax2,n_A1,10*log10(jkb(1,:)),n_A1,10*log10(jkb(2,:)))

grid on
legend('3/1[dB]','3/2[dB]','jkb1[dB]','jkb2[dB]')
title('3diags and jakobians graph in dB')

If this answer is found useful would you please be so kind to consider clicking on

to tag it as correct answer?

Thanks