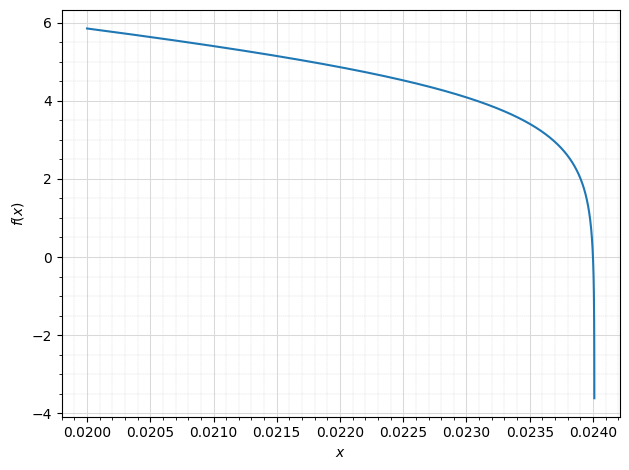
I'm trying to get a solution by running the code below.

Python just "hangs" and won't find a numeric solution. I can use an app on my phone (Desmos) to graph the functions and find a numeric solution easily, 0.024. Does python have limitations when solving for 2 decimal places?

import sympy

x = sympy.symbols('x')
e_1 = x**-0.5
e_2 = -2*sympy.log(0.0001*3.7**-1*diameter**-1 2.51*350000**-1*x**-0.5, 10)
sol = sympy.solve(f_x - g_x, x, 0.024)
num = float(sol[0])
print(num)

CodePudding user response：

Usually, nsolve is the SymPy tool used to numerically solve an equation (or a system of equations). However, I wasn't able to use: it kept raising errors. The problem is that your function is defined on a very small region, and the zero is very close to the boundary:

So, in this case we can try

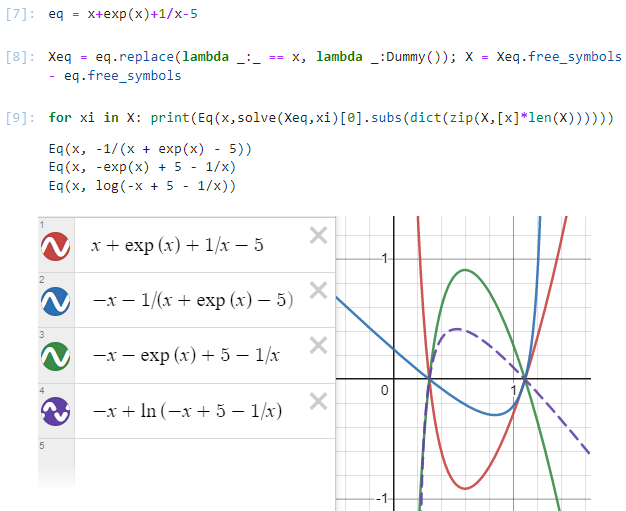
Here is a possibility for a "fixed point form" function:

def fixedpoint_Eqs(eq, x=None):
    """rearrange to give eq in all forms of x = g(x)"""
    f = eq.free_symbols
    fp = []
    if x is None:
        assert len(f) == 1, 'must specify x in this case'
        x = list(f)[0]
    Xeq = eq.replace(lambda _:_ == x, lambda _:Dummy())
    X = Xeq.free_symbols - f
    reps = {xi: x for xi in X}
    for xi in X:
        try: g = solve(Xeq,xi)
        except NotImplementedError: pass
        if len(g) != 1:
            continue
        fp.append(Eq(x, g[0].xreplace(reps)))
    return fp

>>> fixedpoint_Eqs(x exp(x) 1/x-5)
Eq(x, -1/(x   exp(x) - 5))
Eq(x, -exp(x)   5 - 1/x)
Eq(x, log(-x   5 - 1/x))