I want to draw curved arrows, unfortunately, in the function no curvature argument arrows(., curve=) is implemented.

My idea for a solution was to subset an ellipsis. Since plotrix::draw.ellipse() draws lines and I need points for subsetting, I wrote a function arrow_curved() forking the code from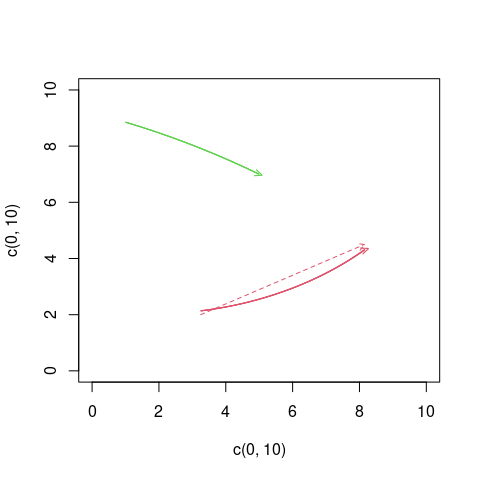

However, you need a little luck to specify the arguments. Ideally, the function would work like arrows(), where we could specify a curvature curve= parameter in addition to x0, y0, x1, y1. Moreover, currently the start and end points only match approximately the values specified in the .xlim= and .ylim= arguments (compare curved red arrow to the straight reference arrow).

Can anybody see a way to improve the function in this regard? Maybe the coordinates can be easily adjusted somehow with the help of mathematics, which is beyond my knowledge.

CodePudding user response：

Your question made me very curious about how to do this, so I had another go. Quite some geometry goes into this, but it was an interesting challenge.

Basically, I realized that if you want to maintain a circular-form to your arc, the distance traveled between two points will depend on how many degrees you specify for the arc. A small number of degrees implies nearly a straight line, while a large number of degrees implies a very round-about way to the second point. My comment regarding the use of splines may make more sense under most cases, but if maintaining a circular form to your arrow is important, then the following seems to do that.

Required functions:

# helper functions to convert between radians and degrees
deg2rad <- function (deg){
  stopifnot(is.numeric(deg))
  (rad <- (pi/180) * deg)
}

rad2deg <- function (rad){
  stopifnot(is.numeric(rad))
  (deg <- rad/(pi/180))
}

# function to calculate the points on an arc between two points
# position 1: x0, y0
# position 2: x1, y1
# number of points in resulting arc line: n
# degrees of the arc connecting the points (positive is counter-clockwise, 
# negative is clockwise): arcdeg
calcArc <- function(x0 = 1, y0 = 1, x1 = 4, y1 = 6, arcdeg = 30, n = 50){
  
  if(abs(arcdeg)>-359.9 & abs(arcdeg)>359.9){stop("angle of arc (arcdeg) must be between -359.9 and 359.9")}
  
  anglerad <- atan2(y = y1-y0, x = x1-x0) # angle between points
  midpt <- list(x = mean(c(x0,x1)), y = mean(c(y0,y1))) # midpoint coordinates of chord
  arcrad <- deg2rad(deg = arcdeg) # angle of arc in radians
  chordlength <- sqrt((x1-x0)^2   (y1-y0)^2) # length between points
  r <- abs((chordlength/2) / sin(arcrad/2)) # radius of circle
  
  # angle from midpoint to circle center
  lut <- data.frame(
    lessthan180 = c(TRUE, TRUE, FALSE, FALSE), 
    sign = c(1, -1, 1, -1), 
    rotation = c(90, -90, -90, 90))
  hit <- which(lut$lessthan180 == (abs(arcdeg) < 180) & lut$sign == sign(arcdeg))
  anglecen <- anglerad   deg2rad(lut$rotation[hit])
  
  # length of midpoint to circle center
  midpt2cenpt <- sqrt(r^2 - (chordlength/2)^2) 
  
  # calculate center point
  cenpt <- list(x = midpt$x   midpt2cenpt*cos(anglecen), 
    y = midpt$y   midpt2cenpt*sin(anglecen))
  
  # angle from circle center to arc
  anglecen2arc <- anglecen   ifelse(abs(arcdeg)<180, deg2rad(180), 0)

  # produce vector of arc with n points
  arc <- data.frame(
    rad = seq(
      from = anglecen2arc - arcrad/2,
      to = anglecen2arc   arcrad/2, 
      length.out = n
    )
  )
  arc$x <- cenpt$x   r*cos(arc$rad)
  arc$y <- cenpt$y   r*sin(arc$rad)
  
  return(arc)
}

# function drawing the results of calcArc as a line or arrow.
# makes a conversion in plotting region units in order to maintain a circular arc
addArc <- function(x0 = 1, y0 = 1, x1 = 4, y1 = 6, arcdeg = 30, n = 50, 
  t = "l", col = 1, lty = 1, lwd = 1, 
  arrowlength = NULL, arrowangle = 30, arrowcode = 2,
  result = FALSE,
  ...){
  
  # calculate arc
  arc <- calcArc(x0 = x0, y0 = y0, x1 = x1, y1 = y1, arcdeg = arcdeg, n = n)

  # calculate arc in device units
  FROM = "user"
  TO = "chars"
  
  x0 <- grconvertX(x0, from = FROM, to = TO)
  x1 <- grconvertX(x1, from = FROM, to = TO)
  y0 <- grconvertY(y0, from = FROM, to = TO)
  y1 <- grconvertY(y1, from = FROM, to = TO)
  arc2 <- calcArc(x0 = x0, y0 = y0, x1 = x1, y1 = y1, arcdeg = arcdeg, n = n)
  names(arc2) <- c("rad", "xusr", "yusr")
  
  arc <- cbind(arc, arc2[,c("xusr", "yusr")])
  
  # convert back to user coordinates
  arc$xusr <- grconvertX(arc$xusr, from = TO, to = FROM)
  arc$yusr <- grconvertY(arc$yusr, from = TO, to = FROM)
  
  lines(yusr ~ xusr, data = arc, t = t, 
    col = col, lty = lty, lwd = lwd, ...)
  if(!is.null(arrowlength)){
    arrows(x0 = arc$xusr[n-1], x1 = arc$xusr[n], y0 = arc$yusr[n-1], y1 = arc$yusr[n], 
      length = arrowlength, code = arrowcode, angle = arrowangle, 
      col = col, lty = lty, lwd = lwd, ...)
  }
  
  if(result){return(arc)}
}

Example 1 - adding several arrow arcs of differing degree between 2 points

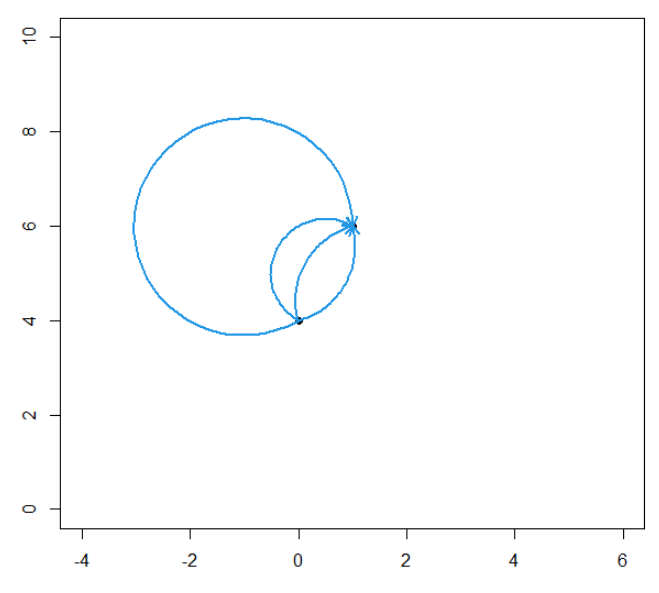
plot(1, t = "n", xlim = c(-4, 6), ylim = c(0,10), xlab = "", ylab = "")
points(x = c(0,1), y = c(4,6), pch = 16, cex = 1)
addArc(x0 = 0, x1 = 1, y0 = 4, y1 = 6, arcdeg = 90, col = 4, arrowlength = 0.1, lwd = 2)
addArc(x0 = 0, x1 = 1, y0 = 4, y1 = 6, arcdeg = -90, col = 4, arrowlength = 0.1, lwd = 2)
addArc(x0 = 0, x1 = 1, y0 = 4, y1 = 6, arcdeg = -180, col = 4, arrowlength = 0.1, lwd = 2)
addArc(x0 = 0, x1 = 1, y0 = 4, y1 = 6, arcdeg = -300, col = 4, arrowlength = 0.1, lwd = 2)

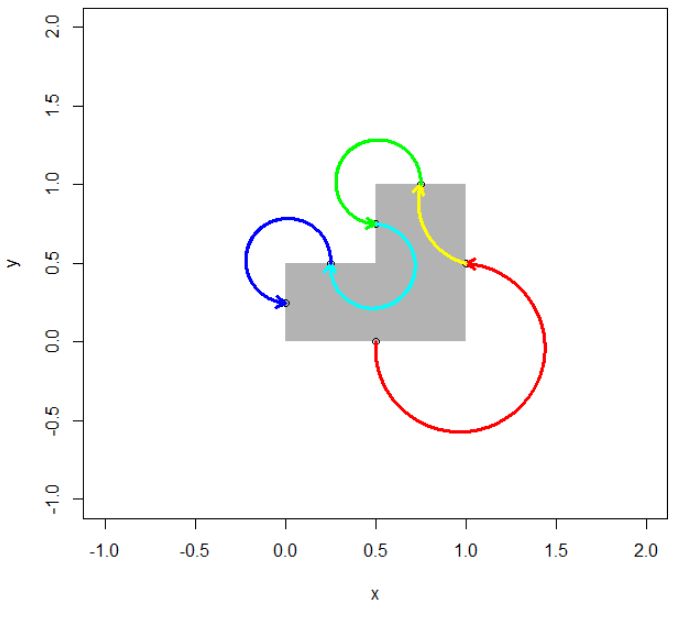
Example 2 - arrows connecting points around a box

df <- data.frame(x = c(0,1,1,0.5,0.5,0, 0), y = c(0,0,1,1,0.5,0.5,0))
dfmid <- data.frame(x = df$x[-nrow(df)]   diff(df$x)/2,
  y = df$y[-nrow(df)]   diff(df$y)/2)
dfmid$arcdeg <- c(270, -90, 270, -270, 270, 270)
dfmid$col <- rainbow(nrow(dfmid))
plot(y ~ x, df, t = "n", xlim = c(-1,2), ylim = c(-1,2))
polygon(x = df$x, y = df$y, col = "grey70", border = NA)
points(y ~ x, dfmid)
for(i in seq(nrow(dfmid)-1)){
  addArc(x0 = dfmid$x[i], y0 = dfmid$y[i], x1 = dfmid$x[i 1], y1 = dfmid$y[i 1], 
    arcdeg = dfmid$arcdeg[i], arrowlength = 0.1, col = dfmid$col[i], 
    lwd = 3, lty = 1, n = 500, t = "l")
}