def getPolynomialFitFunction(points):
    # get x and y vectors
    x = points[:,0]
    y = points[:,1]

    # calculate polynomial
    z = np.polyfit(x, y, 2)
    f = np.poly1d(z)

    # calculate new x's and y'sq
    x_new = np.linspace(x[0], x[-1], 3)
    y_new = f(x_new)

    plt.plot(x,y,'o', x_new, y_new)
    plt.xlim([x[0]-1, x[-1]   1 ])
    plt.show()

    return f

def main():
    arr = []

    for i in range(0, 20):
        arr.append([pow(i,2), -i])
    for i in range(0, 20):
        arr.append([pow(i,2), i])
    
    arr = np.array(arr)
    f = getPolynomialFitFunction(arr)
    print(f(19*19))


if __name__ == "__main__":
    main()

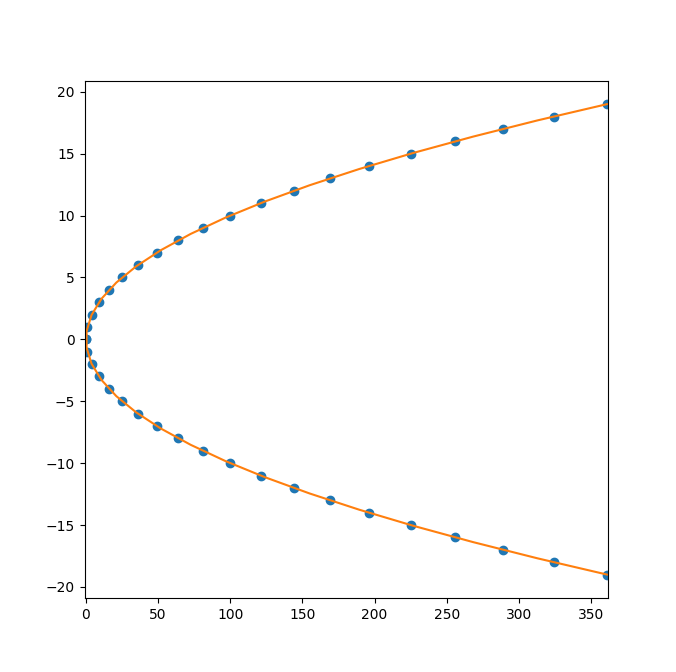
I have written a python script. I fed the polyfit function with parabola of x = y^2 . The result is very disappointing. Output is here