I have a code which gets a number of triangles in an Undirected Graph using matrix multiplication method. Now I would like it to also print these triangles, preferably to print those vertexes. It could be done with third party libraries, e.g. numpy or networkx, but it has to be done with matrix multiplication, as I know that I could do it with naive version.
To make it simplier I will use the easiest adjacency matrix:
[[0, 1, 0, 0],
[1, 0, 1, 1],
[0, 1, 0, 1],
[0, 1, 1, 0]]
it has edges:
x,y
0,1
1,2
1,3
2,3
So the triangle exsists between vertexes 1,2,3 and this is what I would like this program ALSO prints to the console
Now the code, which just prints how many triangles are in this graph:
# num of vertexes
V = 4
# graph from adjacency matrix
graph = [[0, 1, 0, 0],
[1, 0, 1, 1],
[0, 1, 0, 1],
[0, 1, 1, 0]]
# get the vertexes in a dict
vertexes = {}
for i in range(len(graph)):
vertexes[i] = i
print(vertexes)
## >> {0: 0, 1: 1, 2: 2, 3: 3}
# matrix multiplication
def multiply(A, B, C):
global V
for i in range(V):
for j in range(V):
C[i][j] = 0
for k in range(V):
C[i][j] = A[i][k] * B[k][j]
# Utility function to calculate
# trace of a matrix (sum of
# diagonal elements)
def getTrace(graph):
global V
trace = 0
for i in range(V):
trace = graph[i][i]
return trace
# Utility function for calculating
# number of triangles in graph
def triangleInGraph(graph):
global V
# To Store graph^2
aux2 = [[None] * V for _ in range(V)]
# To Store graph^3
aux3 = [[None] * V for i in range(V)]
# Initialising aux
# matrices with 0
for i in range(V):
for j in range(V):
aux2[i][j] = aux3[i][j] = 0
# aux2 is graph^2 now printMatrix(aux2)
multiply(graph, graph, aux2)
# after this multiplication aux3 is
# graph^3 printMatrix(aux3)
multiply(graph, aux2, aux3)
trace = getTrace(aux3)
return trace // 6
print("Total number of Triangle in Graph :",
triangleInGraph(graph))
## >> Total number of Triangle in Graph : 1
CodePudding user response：
The thing is, the information of the triangle (more generally speaking, information of paths between a vertex i and a vertex j) is lost during that matrix multiplication process. All that is stored is that the path exist.
For adjacency matrix itself, whose numbers are the number of length 1 paths between i and j, answer is obvious, because if a path exists, then it has to be edge (i,j). But even in M², when you see number 2 at row i column j of M², well, all you know is that there are 2 length 2 paths connecting i to j. So, that it exists 2 different index k₁ and k₂, such as (i,k₁) and (k₁,j) are edges, and so are (i,k₂) and (k₂, j).
That is exactly why matrix multiplication works (and that is a virtue of coding as explicitly as you did: I don't need to recall you that element M²ᵢⱼ = ΣMᵢₖ×Mₖⱼ
So it is exactly that: 1 for all intermediate vertex k such as (i,k) and (k,j) are both edges. So 1 for all intermediate vertex k such as (i,k),(k,j) is a length 2 path for i to j.
But as you can see, that Σ is just a sum. In a sum, we loose the detail of what contributed to the sum.
In other words, nothing to do from what you computed. You've just computed the number of length-3 path from i to j, for all i and j, and, in particular what you are interested in, the number of length-3 paths from i to i for all i.
So the only solution you have, is to write another algorithm, that does a completely different computation (but makes yours useless: why compute the number of paths, when you have, or you will compute the list of paths?). That computation is a rather classic one: you are just looking for paths from a node to another. Only, those two nodes are the same.
Nevertheless the most classical algorithm (Dijkstra, Ford, ...) are not really useful here (you are not searching the shortest one, and you want all paths, not just one).
One method I can think of, is to start nevertheless ("nevertheless" because I said earlier that your computing of length of path was redundant) from your code. Not that it is the easiest way, but now that your code is here; besides, I allways try to stay as close as possible from the original code
Compute a matrix of path
As I've said earlier, the formula ΣAᵢₖBₖⱼ makes sense: it is computing the number of cases where we have some paths (Aᵢₖ) from i to k and some other paths (Bₖⱼ) from k to j. You just have to do the same thing, but instead of summing a number, sum a list of paths. For the sake of simplicity, here, I'll use lists to store paths. So path i,k,j is stored in a list [i,k,j]. So in each cell of our matrix we have a list of paths, so a list of list (so since our matrix is itself implemented as a list of list, that makes the path matrix a list of list of list of list)
The path matrix (I made up the name just now. But I am pretty sure it has already an official name, since the idea can't be new. And that official name is probably "path matrix") for the initial matrix is very simple: each element is either [] (no path) where Mᵢⱼ is 0, and is [[i,j]] (1 path, i→j) where Mᵢⱼ is 1.
So, let's build it
def adjacencyToPath(M):
P=[[[] for _ in range(len(M))] for _ in range(len(M))]
for i in range(len(M)):
for j in range(len(M)):
if M[i][j]==1:
P[i][j]=[[i,j]]
else:
P[i][j]=[]
return P
Now that you've have that, we just have to follow the same idea as in the matrix multiplication. For example (to use the most complete example, even if out of your scope, since you don't compute more than M³) when you compute M²×M³, and say M⁵ᵢⱼ = ΣM²ᵢₖM³ₖⱼ that means that if M²ᵢₖ is 3 and M³ₖⱼ is 2, then you have 6 paths of length 5 between i and j whose 3rd step is at node k: all the 6 possible combination of the 3 ways to go from i to k in 3 steps and the 2 ways to go from k to j in 2 steps. So, let's do also that for path matrix.
# Args=2 list of paths.
# Returns 1 list of paths
# Ex, if p1=[[1,2,3], [1,4,3]] and p2=[[3,2,4,2], [3,4,5,2]]
# Then returns [[1,2,3,2,4,2], [1,2,3,4,5,2], [1,4,3,2,4,2], [1,4,3,4,5,2]]
def combineListPath(lp1, lp2):
res=[]
for p1 in lp1:
for p2 in lp2:
res.append(p1 p2[1:]) # p2[0] is redundant with p1[-1]
return res
And the path matrix multiplication therefore goes like this
def pathMult(P1, P2):
res=[[[] for _ in range(len(P1))] for _ in range(len(P1))]
for i in range(len(P1)):
for j in range(len(P1)):
for k in range(len(P1)):
res[i][j] = combineListPath(P1[i][k], P2[k][j])
return res
So, all we have to do now, is to use this pathMult function as we use the matrix multiplication. As you computed aux2, let compute pm2
pm=adjacencyToPath(graph)
pm2=pathMult(pm, pm)
and as you computed aux3, let's compute pm3
pm3=pathMult(pm, pm2)
And now, you have in pm3, at each cell pm3[i][j] the list of paths of length 3, from i to j. And in particular, in all pm3[i][i] you have the list of triangles.
Now, the advantage of this method is that it mimics exactly your way of computing the number of paths: we do the exact same thing, but instead of retaining the number of paths, we retain the list of them.
Faster way
Obviously there are more efficient way. For example, you could just search pair (i,j) of connected nodes such as there is a third node k connected to both i and j (with an edge (j,k) and an edge (k,i), making no assumption whether your graph is oriented or not).
def listTriangle(M):
res=[]
for i in range(len(M)):
for j in range(i,len(M)):
if M[i][j]==0: continue
# So, at list point, we know i->j is an edge
for k in range(i,len(M)):
if M[j,k]>0 and M[k,i]>0:
res.append( (i,j,k) )
return res
We assume j≥i and k≥i, because triangles (i,j,k), (j,k,i) and (k,i,j) are the same, and exist all or none.
It could be optimized if we make the assumption that we are always in a non-oriented (or at least symmetric) graph, as you example suggest. In which case, we can assume i≤j≤k for example (since triangles (i,j,k) and (i,k,j) are also the same), turning the 3rd for from for k in range(i, len(M)) to for k in range(j, len(M)). And also if we exclude loops (either because there are none, as in your example, or because we don't want to count them as part of a triangle), then you can make the assumption i<j<k. Which then turns the 2 last loops into for j in range(i 1, len(M)) and for k in range(j 1, len(M)).
Optimisation
Last thing I didn't want to introduce until now, to stay as close as possible to your code. It worth mentioning that python already has some matrix manipulation routines, through numpy and the @ operator. So it is better to take advantage of it (even tho I took advantage of the fact you reinvented the wheel of matrix multiplication to explain my path multiplication).
Your code, for example, becomes
import numpy as np
graph = np.array([[0, 1, 0, 0],
[1, 0, 1, 1],
[0, 1, 0, 1],
[0, 1, 1, 0]])
# Utility function for calculating
# number of triangles in graph
# That is the core of your code
def triangleInGraph(graph):
return (graph @ graph @ graph).trace()//6 # numpy magic
# shorter that your version, isn't it?
print("Total number of Triangle in Graph :",
triangleInGraph(graph))
## >> Total number of Triangle in Graph : 1
Mine is harder to optimize that way, but that can be done. We just have to define a new type, PathList, and define what are multiplication and addition of pathlists.
class PathList:
def __init__(self, pl):
self.l=pl
def __mul__(self, b): # That's my previous pathmult
res=[]
for p1 in self.l:
for p2 in b.l:
res.append(p1 p2[1:])
return PathList(res)
def __add__(self,b): # Just concatenation of the 2 lists
return PathList(self.l b.l)
# For fun, a compact way to print it
def __repr__(self):
res=''
for n in self.l:
one=''
for o in n:
one=one '→' str(o)
res=res ',' one[1:]
return '<' res[1:] '>'
Using list pathlist (which is just the same list of list as before, but with add and mul operators), we can now redefine our adjacencyToPath
def adjacencyToPath(M):
P=[[[] for _ in range(len(M))] for _ in range(len(M))]
for i in range(len(M)):
for j in range(len(M)):
if M[i][j]==1:
P[i][j]=PathList([[i,j]])
else:
P[i][j]=PathList([])
return P
And now, a bit of numpy magic
pm = np.array(adjacencyToPath(graph))
pm3 = pm@pm@pm
triangles = [pm3[i,i] for i in range(len(pm3))]
pm3 is the matrix of all paths from i to j. So pm3[i,i] are the triangles.
Last remark
Some python remarks on your code.
It is better to compute V from your data, that assuming that coder is coherent when they choose V=4 and a graph 4x4. So
V=len(graph)is betterYou don't need
global Vif you don't intend to overwrite V. And it is better to avoid as manyglobalkeywords as possible. I am not repeating a dogma here. I've nothing against a global variable from times to times, if we know what we are doing. Besides, in python, there is already a sort of local structure even for global variables (they are still local to the unit), so it is not as in some languages where global variables are a high risks of collision with libraries symbols. But, well, not need to take the risk of overwriting V.No need neither for the allocate / then write in way you do your matrix multiplication (like for matrix multiplication. You allocate them first, then call matrixmultiplication(source1, source2, dest). You can just return a new matrix. You have a garbage collector now. Well, sometimes it is still a good idea to spare some work to the allocation/garbage collector. Especially if you intended to "recycle" some variables (like in
mult(A,A,B); mult(A,B,C); mult(A,C,B)where B is "recycled")
CodePudding user response：
Since the triangles are defined by a sequence o vertices i,j,k such that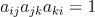 
, we can define the following function:
def find_triangles(adj, n=None):
if n is None:
n = len(adj)
triangles = []
for i in range(n):
for j in range(i 1, n):
for k in range(j 1, n):
if (adj[i][j] and adj[j][k] and adj[k][i]):
triangles.append([i, j, k])
return triangles
print("The triangles are: ", find_triangles(graph, V))
## >> The triangles are: [[1, 2, 3]]