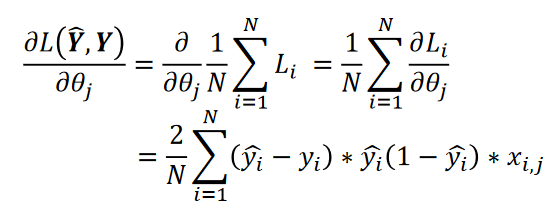I have this code below for my implementation of a gradient descent:

class Neuron():
    def __init__(self):
        #Generate random weight
        self.weights = [np.random.rand() for _ in range(4)]
        self.learning_rate = 0.1

    @staticmethod
    def activation_func(z):
        return ((math.e ** z) - (math.e ** (-z)))/((math.e ** z)   (math.e ** (-z)))

    def get_output(self, inputs):
        s = 0
        inputs_with_bias = [1]   [*inputs]
        for i,j in zip(inputs_with_bias, self.weights):
            s  = i*j
        return self.activation_func(s) 

    def calculate_loss(self, training_dataset, training_result):
        loss = [0] * 4
        for i in range( len(training_result) ):
            res = training_result[i]
            out = self.get_output(training_dataset[i])
            k = (out - res) * (out) * (1 - out)
            cord = [1]   [*training_dataset[i]]
            for j in range(len(cord)):
                loss[j]  = cord[j] * k

        return [i * ( 2/len(training_dataset) ) for i in loss]

    def gradient_descent(self, training_dataset, training_result):
        loss = self.calculate_loss(training_dataset, training_result)
        self.weights = [j-self.learning_rate*i for i,j in zip(loss, self.weights)]

    def make_predictions(self, inputs):
        return [1 if self.get_output(i) >= 0 else -1 for i in inputs]

#Training code:
for i in range(100):
    neuron.gradient_descent(points, expected_res)
    actual_res = neuron.make_predictions(points)

    loss = sum((i-j)**2 for i,j in zip(expected_res, actual_res))
    print("Loss: ",loss)

I'm trying to use it to categorize a set of 3D points into two distinct groups, which are labelled -1 and 1 respectively. The calculate_loss() function is implemented according to the derivative (gradient) of the object loss function:

I could not find any logical error within the code, however, when I run the gradient_descent() function multiple times in order to train the neuron, the loss function increases and the accuracy of the model decreases as well. The data itself is randomly generated 3d points with distinct means, so it should not be causing this behavior.

Edit 1: I've done some further poke around and it seems to be the bug is associated with the activation function, as changing it to sigmoid and the categories to 0 and 1 seems to consistently work, but not with tanh and -1 and 1, absolutely no idea why this is the case though.

CodePudding user response：

I see the backpropagation equation used in the code is for sigmoidal activation not for tanh(), hence the code works for sigmoid function only.

Basically, the backpropagation step invokes the chain rule for differentiation to calculate the change in network weights for a given los value. This chain rule requires you to substitute the derivative of the sigmoid function into the calculation of the Jacobian.

The derivative of a sigmoid function is y'(x) = y(x)*(1-y(x)) which gives you the final form in the above equation.

The derivative of tanh(x) function is tanh'(x)=1-tanh^2(x). Hence this is what will go into the backprop equation:

k = (out-res)*(1-out**2) 

CodePudding user response：

Have you tried reducing the learning rate (=0.1)? If your loss is increasing with every iteration, it is likely that the gradient descent steps are too large and cause the weights to diverge from the optimium. One way to verify this would be to print the gradient values for every iteration and check if they are descreasing.

CodePudding user response：

Shifting tanh output from -1 to 1 into 0 to 1 solved it, though I'm no idea why. Maybe it has something to do with the direction of the gradient descent.