Gradient descent from mathematical ideation for sum of squared errors-CodePudding

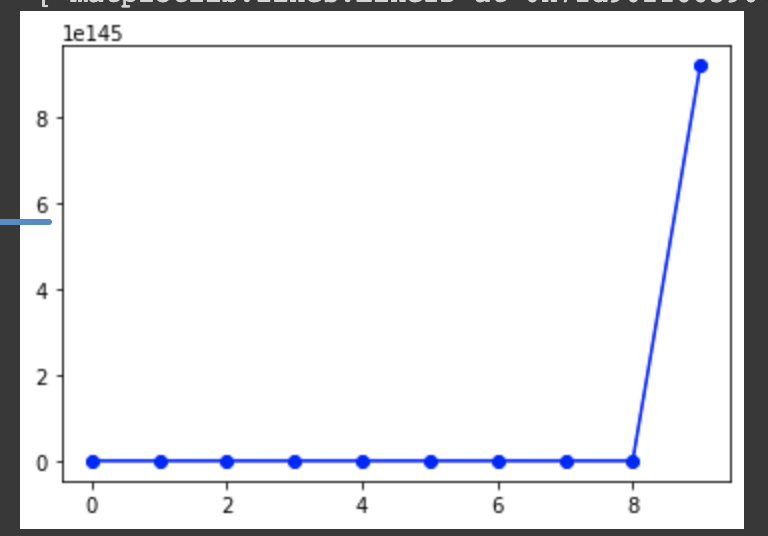
I have the following gradient descent algorithm that I derived mathematically for sum of squared errors. However, when I implement it, the losses increase as shown below. I'm trying to understand the error but can't seem to find the mathematical fallacy as the dimensions and derivation line up, so I'm not quite sure what's going on.

I also used a randomly generated dataset as such:

import pandas as pd
import numpy as np

testing = pd.DataFrame(np.random.randint(0,100,size=(100, 3)), columns=list('ABC'))
testing.insert(0, 'W_o', 1) # W initial 
testing.insert(-1, 'Y', np.random.randint(0,4,size=(100, 1))) #target

import matplotlib.pyplot as plt

def grad_descent_SSE(X,y,T,lr):
  
  # Shape of dataset
  m,n = X.shape

  #Initialize parameters
  W = np.zeros(n)
  # W = OLS[0]

  # Track loss over time
  f = np.zeros(T)

  for i in range(T):

    # Loss for the current parameter vector W
    f[i] = 0.5*np.linalg.norm(X.dot(W) - y)**2

    # Compute steepest ascent at f(W)
    W_update = np.matmul(X.T,np.matmul(X,W)-y)
    # W_update = np.transpose(X).dot(X.dot(W) - y)

    # Calculating the updated weights 
    W = W - lr * W_update

  return W,f, plt.plot(f,'b-o')

CodePudding user response：

Short Answer : You are probably using a larger learning rate. Try reducing the learning rate.

Long Answer : Let's take 20 random samples, each having a dimension of 5. Then our X will have the dimension of (20,5). Let's assume W_t is the true weight we are aiming to reach. If we ignore the bias, then the linear equation becomes y = W_t*X.

n = 5
m = 20 
X = np.random.random((m,n))
W_t = np.random.random(n)
y = np.matmul(X,W_t)

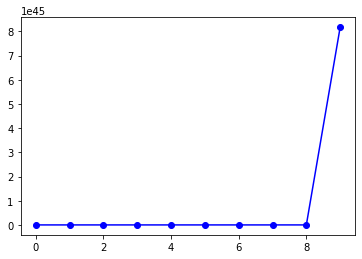
If I use your function with T=10 and lr=10

grad_descent_SSE(X,y,10,10)

I get a graph similar as you.

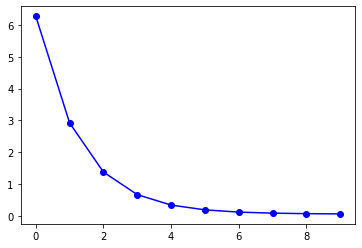
When I reduce the learning rate to 0.01 (lr=0.01), the gradient is descending.