I'm trying to plot a multi-equation ODE from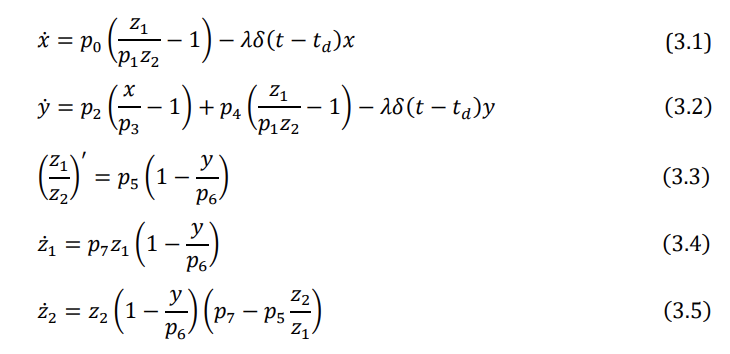

CodePudding user response：

You have to implement a system ODE function

def sys(t,u):
    x,y,z1,z2 = u
    v1 = z1/(p1*z2)-1
    v2 = 1-y/p6
    return p0*v1, p2*(x/p3-1) p4*v1, p7*z1*v2, (p7-p5*z2/z1)*z2*v2

#integrate to jump
sol1 = solve_ivp(sys,(t0,td),u0,**options)
# implement the jump
x,y,z1,z2 = sol1.y[:,-1]
fac = (2-λ)/(2 λ); 
x*=fac; y*=fac
ud = [x,y,z1,z2]
# restart integration
sol2 = solve_ivp(sys,(td,tf),ud,**options)

options is a dictionary for the method, tolerances, etc., see documentation. Then evaluate the solutions.

CodePudding user response：

Thank you Lutz Lehmann, I solved it based on your answer. On a side note, equation 3.3 isn't redundant, I should have clarified that it's a term for the amount of pure silver in each coin. So it's an independent value (weird way of defining it in the paper, I agree).

Here is the solution I ended up using:

def dSdt(t,S):
x,y,z1,z2,z1_z2 = S

xn = p0*((z1_z2/p1)-1)

yn = p2*((x/p3)-1)   p4*((z1_z2/p1)-1) 

z1n = p7*z1*(1-(y/p6))

z2n = z2*(1-(y/p6))*(p7-p5*z1_z2)

z1_z2n = p5*(1-(y/p6))

return [xn,yn,z1n,z2n,z1_z2n]

# Before td
t1 = np.linspace(t0,395,abs(t0) 395,dtype=int)
S0_1 = [x_t0,y_t0,z1_t0,z2_t0,z1_div_z2_t0]
sol1 = odeint(dSdt,y0=S0_1,t=t1,tfirst=True)

# Handle division at td
sol1[-1][0] *= λ 
sol1[-1][1] *= λ
S0_2 = sol1.T[:,-1]

# After td
t2 = np.linspace(start=396,stop=500,num=500-396,dtype=int)
sol2 = odeint(dSdt,y0=S0_2,t=t2,tfirst=True)
sol= np.concatenate((sol1,sol2))
t = np.concatenate((t1,t2))