I'm reading data from a sensor. The sensor give an array of points (x,y). But as you can see in the image, there is a lot of noise:

.

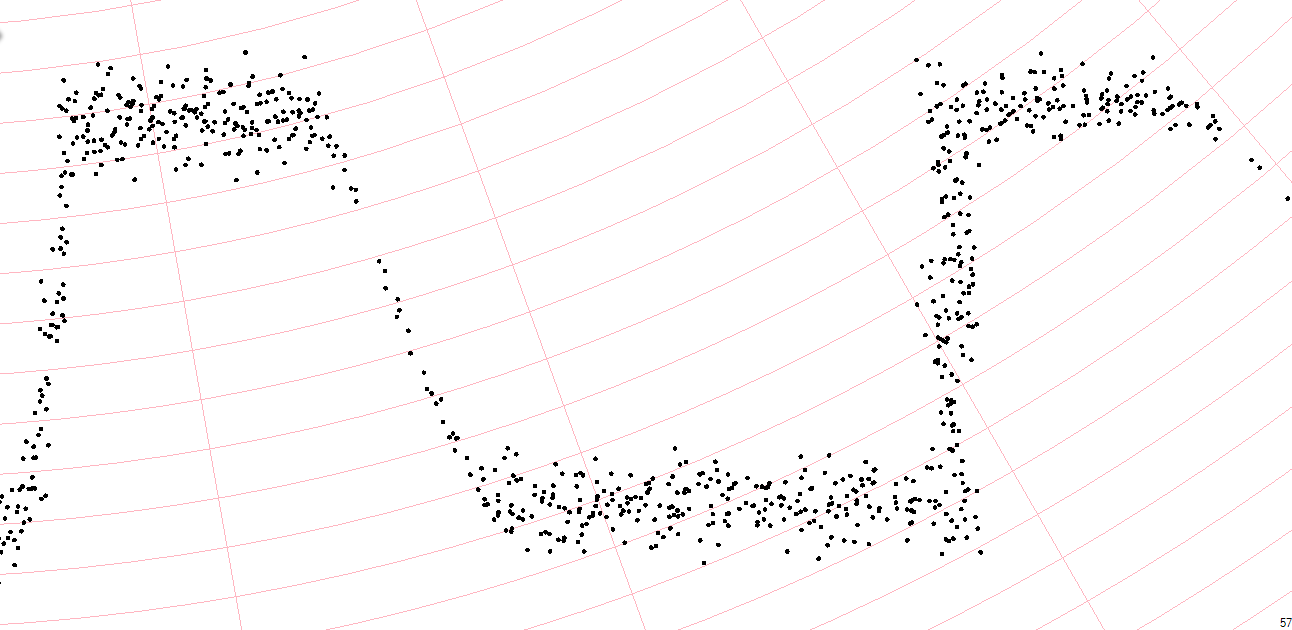I need to clean the data in a way that the data filtered, give a few points . Using something like Median,adjacent averaging, mean of the xy points or an algorith that removes the noise. I know that there are a bunch of libraries in Python that make the work automatically. All the auto libraries that I found are base on image analysis and I think they do not work for this case because this is different, these are points (x,y) in a dataset.

point-cloud noise cleaned:

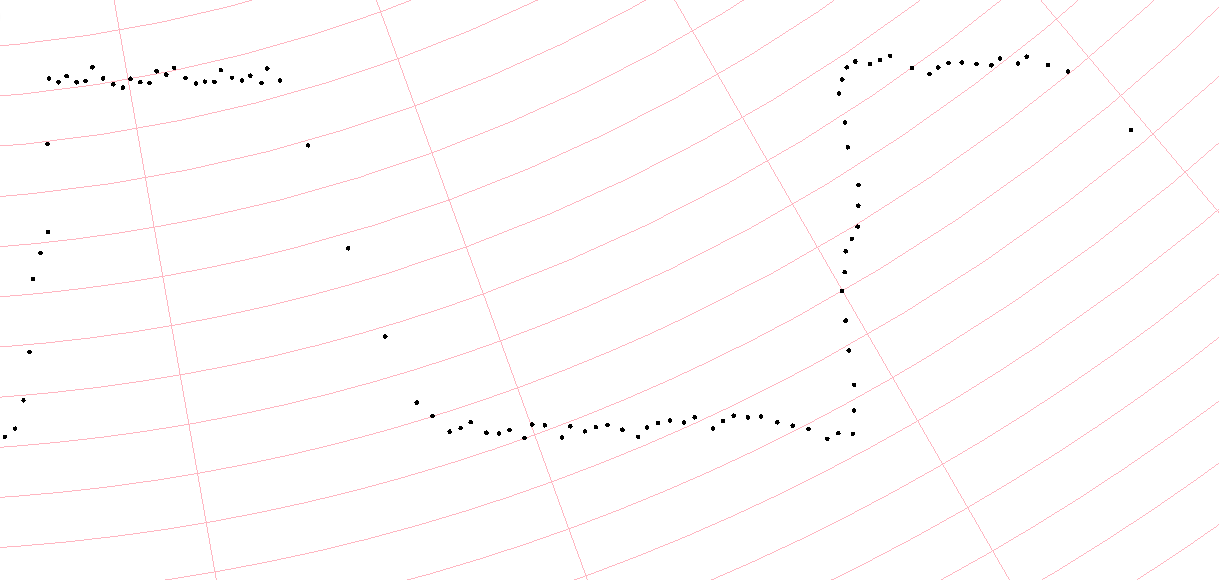
PD: I wanted to do the median of the points but i got confused when i tried with an bidimensional array (this mean ListOfPoints[[x,y],[x,y],[x,y],[x,y],[x,y],[x,y]]) I didn't know how to make that calculation with for or while to iterate and make the calc. I preffer C#, but if there is a solution in other language without libraries, I would be open to it.

CodePudding user response：

One of the methods you can use is k_means algorithm. This picture briefly explains this algorithm k_means

This link fully explains the k_means algorithm. Also, how to create a loop on the input data. I don't think any additional explanation is needed k_means algorithm

K_menans algorithm is very simple and you will understand it with the first Google search

CodePudding user response：

You could try doing a weighted average of the Y-value at sampled X-positions. Something like this:

List<Point2> filtered_points = new List<Point2>();
for (int x = xmin; x <= xmax; x  )
{
    double weight_sum = 0;
    List<double> weights = new List<double>();
    foreach (Point2 p in point_list)
    {
        double w = 1.0/((p.x - x)*(p.x - x)   1e-3);
        weights.Add(w);
        weight_sum  = w;
    }

    double y = 0;
    for (int i = 0; i < point_list.Count; i  )
    {
        y  = weights[i]*point_list[i].y / weight_sum;
    }
    filtered_points.Add(new Point2(x, y));
}

You would probably need to tune the weights to get nice results. Also, in the example I am using a quadratic decay, but other weighting functions can be used (linear decay, gaussian function...)