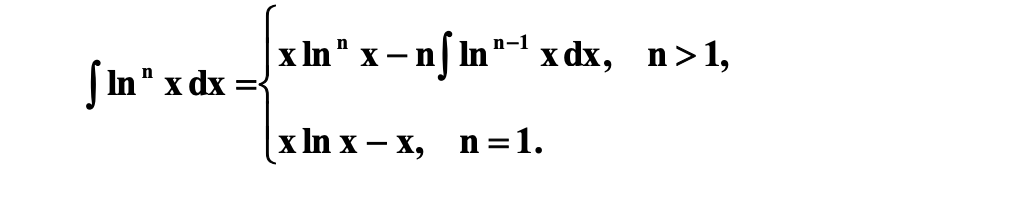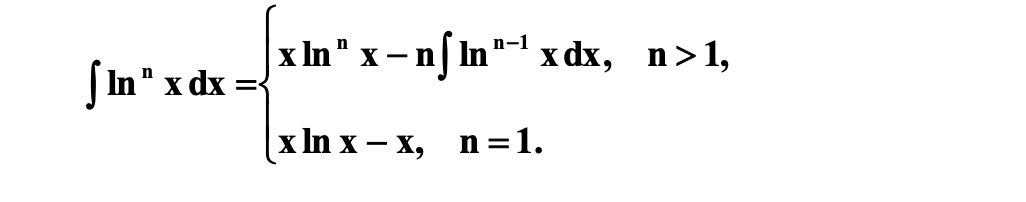i am not sure how to resolve this math problem. what should i recall and where did i miss something. i have tried different opportunities. i think i just call not existing index or something like that..

#include <iostream>
using namespace std;
double recur(int n, int x);
double x;
int number;

int main()
{
    cout << "enter n: " ;
    cin >> number;
    cout << endl;
    do
    {
        cout << "enter float x!=0: ";
        cin >> x;
        cout << endl;
    } while (x==0);
    cout << "recur(" << number << "," << x << ")=" << recur(number, x) << endl;
    system("pause");
}
double recur(int n, int x)
{
    if (n > 1) return (x * recur(n, x - n) * recur(n - 1, x));
    else if( n == 1) return x * recur(n,x) - x;
    else return 1;
}

Formula:

CodePudding user response：

For formula:

It's implementation:

#include <iostream>
#include<cmath>
using namespace std;
double recur(int n, int x);
double x;
int number;

int main()
{
    cout << "enter n: " ;
    cin >> number;
    cout << endl;
    do
    {
        cout << "enter float x!=0: ";
        cin >> x;
        cout << endl;
    } while (x==0);
    cout << "recur(" << number << "," << x << ")=" << recur(number, x) << endl;
    system("pause");
}
double recur(int n, int x)
{
    if (n > 1) return (x*(pow(log(x),n)) - n*(recur(n-1,x)));
    else if( n == 1) return x * log(x) - x;
}

For n>1 line
(x*(pow(log(x),n)) = x*(ln x)^n
n*(recur(n-1,x)) = n* integral( (lnx)^(n-1) ) <- In next recursion call one power will get reduced

For n=1 line
x * log(x) - x = xlnx - x <- base condition(where recursive call will stop)

In this implementation recur(n,x) denotes integration of (lnx)^n w.r.t x.

CodePudding user response：

Your integral isn't the same as the log portion, so you should probably split that out.

double ln_n(int n, double x) {
    while (n --> 0) x = log(x);
    return x;
}

double integral(int n, double x) {
    if (n > 0) return (x * ln_n(n, x)) - (n * integral(n - 1, x));
    return x;
}

See it live