How can vectorize a function that takes two arrays as input?-CodePudding

Assume I have a 3D numpy array $y_{n \times m \times p}$ and a 1D numpy array$x_{p \times 1}$, I want to apply the function 'PyOLS' on each slice of $y$ (i.e., $y[i, j, :]$) and $x$. How can I vectorize this operation in Python?

The following is an example code:

import numpy as np
def PyOLS(xvec, yvec):
   n = xvec.shape[0]
   X = np.c_[xvec, np.ones(n)]
   betas = np.dot(np.linalg.inv(np.dot(X.T, X)), np.dot(X.T, yvec))
   return betas   

n = 20
m = 20
p = 7
x = np.random.rand(n, m, p)
y = np.random.rand(p)

res = np.zeros((n, m))

for i in range(n):
    for j in range(m):
       cx = x[i, j, :]
       b = PyOLS(cx, y)
       res[i, j] = b[0]

How can I vectorize the for loop above to make the code faster, since the 3D array x are very large in my work?

CodePudding user response：

As @relent95 properly said, you can vectorize your approach using an already expanded array for x with the following function:

Vectorized approach

def PyOLS_vectorized(x, y):
    # You could extract this out of the function if done previously
    x2 = np.ones((x.shape   (2,)))
    x2[...,0] = x

    betas = np.einsum(
        "...lk,...l",
        np.linalg.inv(np.einsum("...lk,...lm", x2, x2)),
        np.einsum("...kl,k", x2, y)
                      )
    return betas[...,0]

I really like to use the einsum function because it eases simple array calculations as I can actually see what indices are being summed (I tend to mess them up), as well as for being an (usually) efficient way to operate with arrays. If you prefer matmul if would be more or less the same. Even vectorized, you can see we are kind of wasting resources by computing the whole betas array and then just using the first element; all in all, does not seem a very elegant solution.

However, I'd like to let you know that there is an alternative way of optimizing this, and that is algebraically. If you already know this and the question is just a purely vectorization exercise, feel free to ignore the rest of my answer (I enjoyed worked on it anyways :) ).

Algebraic (and vectorized) approach

Basically, it is not necessary to calculate the inverse (which is the heaviest stuff going on here I assume), because it has an analytical form in this easy case. I did some good ol' calculations with pencil and paper and got an analytical solution. Given your arrays xvec and yvec (I'll denote them x and y), your b[0] element can be expressed as (I'll use LaTeX notation as you seem used to it):

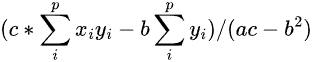
where p is the size of vector y, and a, b and c are the (0,0), (0,1) and (1,0) - the matrix is symmetric-, and (1,1) elements of the np.dot(X.T, X) matrix, respectively. These are actually:

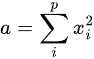
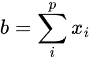
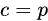
With this equations at hand, I came up with the following function (note this computes directly the element b[0] of b:

def PyOLS_algVectorized(x,y):

    a = np.einsum("...i,...i", x, x)   # shape (n,m)
    b = x.sum(-1)       #  shape (n,m)
    c = x.shape[-1]     #  p

    return (c*np.einsum("...i,i", x, y) - b*y.sum(-1)) / (a*c - b**2)

Now, for the comparison in computation times, I tested it for an arbitrary array x of shape (300, 200, 100), y thus being (100,) and got the following results:

Original function: 3.15 s ± 84 ms per loop (mean ± std. dev. of 7 runs, 1 loop each).
Vectorized function: 837 ms ± 14.3 ms per loop (mean ± std. dev. of 7 runs, 1 loop each).
Algebraically-simplified and vectorized function: 9.74 ms ± 256 µs per loop (mean ± std. dev. of 7 runs, 100 loops each).

As you can see, we obtain an improvement with respect the loopy function of 1 order of magnitude and 3 orders of magnitude(!) using the vectorized approach and algebraically derived approach, respectively. I think the vectorized functions will work for any shape array of x given that the last dimension matches for both x and y. Note that the vectorized approaches requires more memory, so if your arrays are extremely huge and your system's RAM can't hold the arrays, perhaps you should try Numba and keep the loopy version!