Bootstrap Distribution of slope on Linear Regression-CodePudding

Having trouble producing a vector (e.g. "bootdist") containing a bootstrap distribution of 1000 values of the slope of the linear regression of y on x.

I have written the following to fit a linear regression on the given data:

lm.out <- lm(y ~ x)
coef(lm.out)
ypred <- predict(lm.out)
resids <- y - ypred
SSE <- sum(resids^2)
print(paste("Error sum of squares is", SSE))
summary(lm.out)

length(x)

However, unsure how to proceed from here. Any tips on how to apply to bootstrap would be appreciated, thanks!

Data

x <- c(1, 1.5, 2, 3, 4, 4.5, 5, 5.5, 6, 6.5, 7, 8, 9, 10, 11, 12, 
       13, 14, 15)
y <- c(21.9, 27.8, 42.8, 48, 52.5, 52, 53.1, 46.1, 42, 39.9, 38.1, 
       34, 33.8, 30, 26.1, 24, 20, 11.1, 6.3)

CodePudding user response：

library(boot)

x <- c(1, 1.5, 2, 3, 4, 4.5, 5, 5.5, 6, 6.5, 7, 8, 9, 10, 11, 12, 13, 14, 15)
y <- c(21.9, 27.8, 42.8, 48.0, 52.5, 52.0, 53.1, 46.1, 42.0, 39.9, 38.1, 34.0, 33.8, 30.0, 26.1, 24.0, 20.0, 11.1, 6.3)
df <- data.frame(x, y) 

boot_coef <- function(df, idx) {
  x <- df[ idx, 'x' ]
  y <- df[ idx, 'y' ]
  lm.out <- lm(y ~ x)
  coef(lm.out)[[ 2 ]]
}

bs <- boot(data = df, statistic = boot_coef, R = 999)
print(bs)
bs.ci <- boot.ci(boot.out = bs)
print(bs.ci)

CodePudding user response：

What you want is to sample y and x with replacement, and fit the linear model with those new values 1000 times.

Usually we write a function FUN that performs one bootstrap replication and returns the coefficients. Next we repeatedly evaluate FUN and store the results in a matrix r. Best we set a seed beforehand to make the result reproducible. Finally, from r we extract the slope to get the desired bootstrap distribution.

FUN <- \() {
  i <- sample(seq_len(length(x)), replace=TRUE)
  y <- y[i]
  x <- x[i]
  lm(y ~ x)$coefficients
}

set.seed(42)
r <- t(replicate(1e3, FUN()))

head(r, 3)
#      (Intercept)         x
# [1,]    54.45359 -2.602331
# [2,]    47.10187 -1.905300
# [3,]    47.30847 -1.510952

bootdist <- r[, 'x']

head(bootdist)
# [1] -2.602331 -1.905300 -1.510952 -2.919127 -2.357821 -2.320225

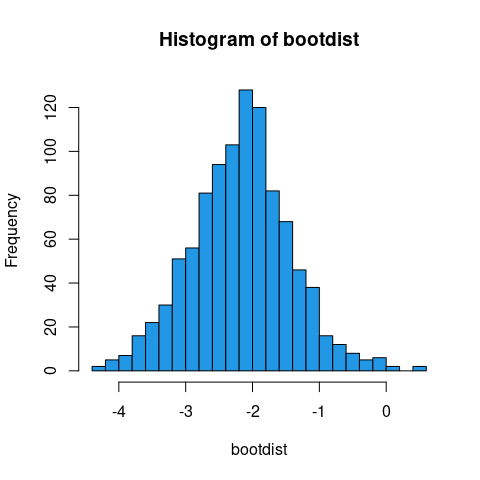
hist(bootdist, 'FD', col=4)

We can also wrap this in a function that in addition to the usual summarry.lm returns the SSR, bootstrap SE and CI, as well as invisibly the bootdist vector for further usage.

bfun <- \(x, y, R=1e3, seed=42, hist=TRUE) {
  fit <- lm(y ~ x)
  resids <- y - fit$fitted
  ssr <- sum(resids^2)
  sfit <- summary(fit)
  FUN <- \() {
    i <- sample(seq_len(length(x)), replace=TRUE)
    y <- y[i]
    x <- x[i]
    lm(y ~ x)$coefficients
  }
  set.seed(seed)
  r <- t(replicate(R, FUN()))
  bootdist <- r[, 2]
  if (hist) {
    hist(bootdist, breaks='FD', col=4)
  }
  bse <- as.matrix(apply(r, 2, sd))
  bci <- t(apply(r, 2, quantile, c(.025, .975)))
  print(sfit)
  cat('Residual sum of squares:\t', ssr, '\n')
  cat('\nBootstrap standard errors:\n')
  print(bse)
  cat('\nBootstrap confidence intervals:\n')
  print(bci)
  invisible(return(bootdist))
}

Output

b <- bfun(x, y)
# Call:
# lm(formula = y ~ x)
# 
# Residuals:
#     Min      1Q  Median      3Q     Max 
# -25.875  -2.270   1.755   4.820  14.005 
# 
# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)   49.945      4.795  10.417 8.48e-09 ***
# x             -2.170      0.572  -3.794  0.00145 ** 
# ---
# Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# Residual standard error: 10.43 on 17 degrees of freedom
# Multiple R-squared:  0.4585,  Adjusted R-squared:  0.4266 
# F-statistic: 14.39 on 1 and 17 DF,  p-value: 0.00145
# 
# Residual sum of squares:   1850.325 
# 
# Bootstrap standard errors:
#                  [,1]
# (Intercept) 6.8447017
# x           0.7407192
# 
# Bootstrap confidence intervals:
#                  2.5%      97.5%
# (Intercept) 37.763470 65.1040062
# x           -3.676248 -0.6528697

head(b)
# [1] -2.602331 -1.905300 -1.510952 -2.919127 -2.357821 -2.320225