How to find peaks in a noisy signal or estimate its number?-CodePudding

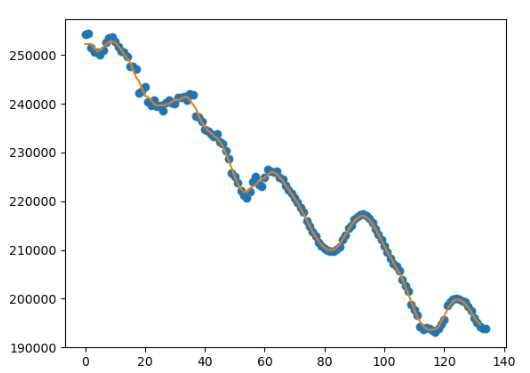
I have a series of signals, sample data looks like this:

We can see that there are 5 peaks there. I can assume that there won't be more than 1 pick every 10 samples, usually there is one pick every 20 to 40 samples.

I was trying to fit a polynomial and then use scipy.signal.find_peaks and it kind of works but I have to choose different numbers of spline knots to approximate each series correctly and the number of knots correlates to the number of peaks so I sort of ended up where I begun - but now I'd need only a rough idea about the number of peaks.

Then I tried it by dividing the signal into parts:

window = 10     # the smallest range potentially containing whole peak
parts = np.array_split(data, len(data)//window)  # divide data set into parts
lengths = []
d = np.nan
for i in parts:
    d = abs(i.max() - i.min())
    lengths.append(d)  # differences between max and min values in each part
av = sum(lengths)/len(lengths)
for i in lengths:
    if i < some_tolerance_fraction*av:
        window = window 1  # make part for next check 2 times bigger
        break

The idea was that the difference between min and max values in these parts should be smaller than the height of an actual pick I'm looking for unless the parts are large enough to contain whole peak - then the differences should be similar in each part and the average should also be similar to the actual height of the pick.

But this doesn't work at all and possibly doesn't even make sense - depending on the tolerance it divides window all the time or doesn't divide it at all.

this is the array from the image:

array([254256., 254390., 251546., 250561., 250603., 250128., 251000.,
   252612., 253552., 253776., 252843., 251800., 250808., 250569.,
   249804., 247755., 247685., 247111., 242320., 242580., 243462.,
   240383., 239689., 240730., 239508., 239604., 238544., 240174.,
   240806., 240218., 239956., 241325., 241343., 241532., 240696.,
   242064., 241830., 237569., 237392., 236353., 234819., 234430.,
   233890., 233215., 233745., 232159., 231778., 230307., 228754.,
   225823., 225139., 223737., 222078., 221188., 220669., 221944.,
   223928., 224996., 223405., 223018., 224966., 226590., 226166.,
   226012., 226192., 224900., 224439., 223179., 222375., 221509.,
   220734., 219686., 218656., 217792., 215934., 214829., 213673.,
   212837., 211604., 210748., 210216., 209974., 209659., 209707.,
   210131., 210663., 212113., 213078., 214476., 215087., 216220.,
   216831., 217286., 217373., 217030., 216491., 215642., 214249.,
   213273., 212148., 210846., 209570., 208202., 207165., 206677.,
   205703., 203837., 202620., 201530., 198812., 197654., 196506.,
   194163., 193736., 193945., 193785., 193417., 193044., 193768.,
   194690., 195739., 198592., 199237., 199932., 200142., 199859.,
   199593., 199337., 198403., 197500., 195988., 195114., 194278.,
   193837., 193861.])

CodePudding user response：

I would use find_peaks of scipy but filtering the signal with a moving average mean:

import numpy as np
import matplotlib.pyplot as plt

arr = np.array([254256., 254390., 251546., 250561., 250603., 250128., 251000.,
   252612., 253552., 253776., 252843., 251800., 250808., 250569.,
   249804., 247755., 247685., 247111., 242320., 242580., 243462.,
   240383., 239689., 240730., 239508., 239604., 238544., 240174.,
   240806., 240218., 239956., 241325., 241343., 241532., 240696.,
   242064., 241830., 237569., 237392., 236353., 234819., 234430.,
   233890., 233215., 233745., 232159., 231778., 230307., 228754.,
   225823., 225139., 223737., 222078., 221188., 220669., 221944.,
   223928., 224996., 223405., 223018., 224966., 226590., 226166.,
   226012., 226192., 224900., 224439., 223179., 222375., 221509.,
   220734., 219686., 218656., 217792., 215934., 214829., 213673.,
   212837., 211604., 210748., 210216., 209974., 209659., 209707.,
   210131., 210663., 212113., 213078., 214476., 215087., 216220.,
   216831., 217286., 217373., 217030., 216491., 215642., 214249.,
   213273., 212148., 210846., 209570., 208202., 207165., 206677.,
   205703., 203837., 202620., 201530., 198812., 197654., 196506.,
   194163., 193736., 193945., 193785., 193417., 193044., 193768.,
   194690., 195739., 198592., 199237., 199932., 200142., 199859.,
   199593., 199337., 198403., 197500., 195988., 195114., 194278.,
   193837., 193861.])



def moving_average(x, w):
    """calculate moving average with window size w"""
    return np.convolve(x, np.ones(w), 'valid') / w

#moving average with size 5
n=5
arr_f = moving_average(arr, 5)
#to show in same plot
arr_f_ext= np.hstack([np.ones(n//2)*arr_f[0],arr_f])
plt.figure()
plt.plot(arr,'o')
plt.plot(arr_f_ext)

This will show:

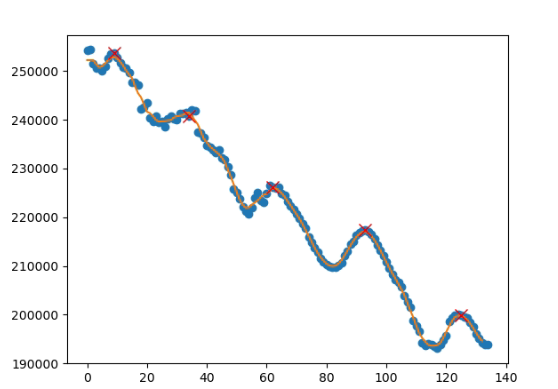
Then find peaks:


from scipy.signal import find_peaks

#n//2 is the offset of the averaged signal (2 in this example)
peaks =find_peaks(arr_f)[0]   n//2

plt.plot(peaks,arr[peaks],'xr',ms=10)

wich will show:

Note that,

the filtered signal will have a delay of n/2 samples (rounding down) so add n//2 to the peaks finded in filtered signal.

2)the filtered signal does not have the same values that the original, but same behaviour, Then to extract peak value use the original signal.

CodePudding user response：

My informal definition of a peak is a point surrounded by two vectors, one ascending and one descending. It's pretty easy to implement it by iterating the array and comparing two neighbouring segments.
If they are both in the same direction, we merge the 2 segments by deleting the middle point.
To determine if they are in the same direction, I used multiplication. The product is positive if the 2 segments are in same direction. At the end, every point will be a peak (we cannot determine for the first and last two).

i = 0 # position cursor at beginning
while i <= (len(t)-3):
  if (t[i] - t[i 1]) * (t[i 1] - t[i 2]) >= 0:
    # Same direction: join 2 segments by removing the middlepoint.
    # This test also include the case of an horizontal segment \
    # formed by the first 2 points. We remove the second.
    del( t[i 1])
  else:
    # different directions. Delete nothing. Move cursor by 1
    i  = 1

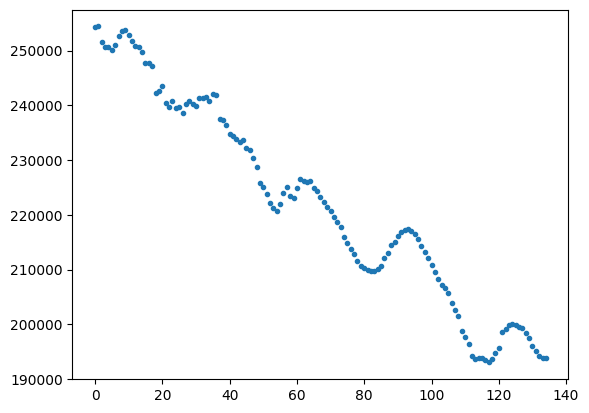
see plot. You can see the reduction from 135 to 34 points.
Each blue mark is a peak. Some of these peaks are non-significant and some more filtering is required. But the best method depend on your application. You may filter on vertical distance between 2 adjacent peaks or the horizontal distance between 2 adjacent peaks. For this last case, we need the x value of each peak so I rewrote the program using x-y data points.

t0 = [254256, 254390, 251546, 250561, 250603, 250128, 251000,
   252612, 253552, 253776, 252843, 251800, 250808, 250569,
   249804, 247755, 247685, 247111, 242320, 242580, 243462,
   240383, 239689, 240730, 239508, 239604, 238544, 240174,
   240806, 240218, 239956, 241325, 241343, 241532, 240696,
   242064, 241830, 237569, 237392, 236353, 234819, 234430,
   233890, 233215, 233745, 232159, 231778, 230307, 228754,
   225823, 225139, 223737, 222078, 221188, 220669, 221944,
   223928, 224996, 223405, 223018, 224966, 226590, 226166,
   226012, 226192, 224900, 224439, 223179, 222375, 221509,
   220734, 219686, 218656, 217792, 215934, 214829, 213673,
   212837, 211604, 210748, 210216, 209974, 209659, 209707,
   210131, 210663, 212113, 213078, 214476, 215087, 216220,
   216831, 217286, 217373, 217030, 216491, 215642, 214249,
   213273, 212148, 210846, 209570, 208202, 207165, 206677,
   205703, 203837, 202620, 201530, 198812, 197654, 196506,
   194163, 193736, 193945, 193785, 193417, 193044, 193768,
   194690, 195739, 198592, 199237, 199932, 200142, 199859,
   199593, 199337, 198403, 197500, 195988, 195114, 194278,
   193837, 193861]

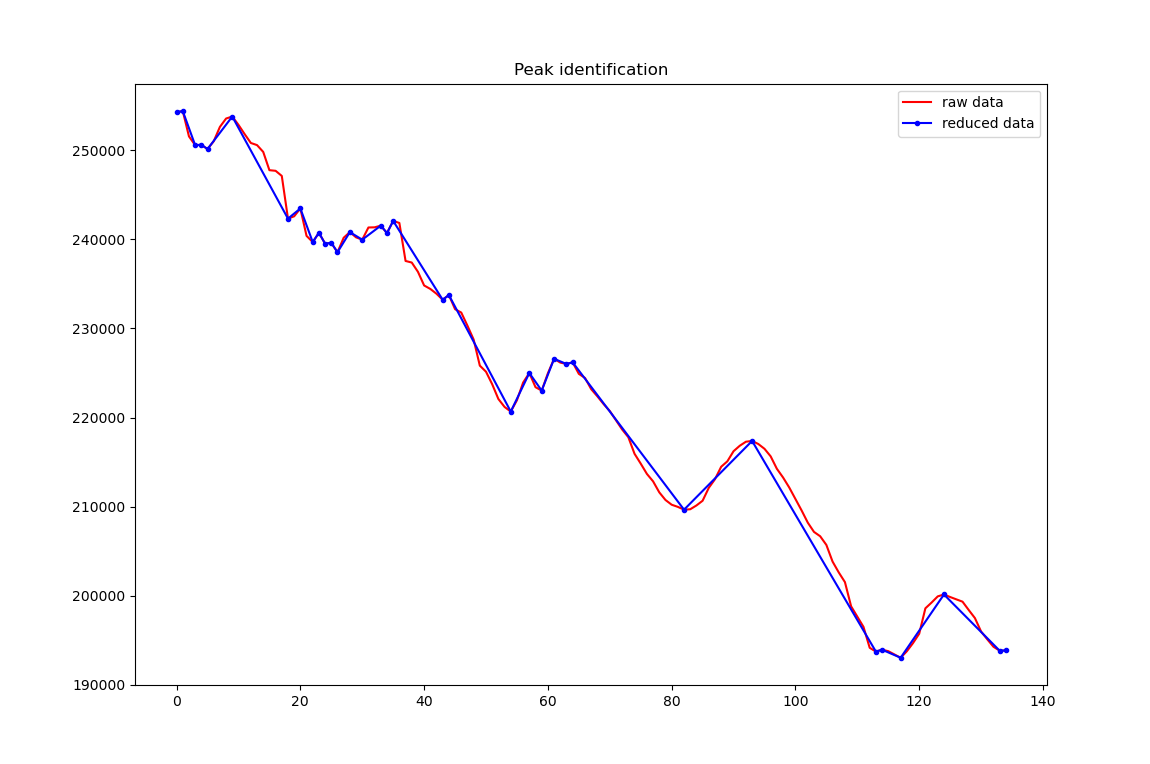
def graph( t1, t2):
  import matplotlib.pyplot as plt
  fig=plt.figure()
  plt.plot( [p[0] for p in t1], [p[1] for p in t1], color='r', label="raw data")
  plt.plot( [p[0] for p in t2], [p[1] for p in t2], marker='.', color='b', label="reduced data")
  plt.title('Peak identification')
  plt.legend()
  plt.show()

def reduce( t):
  i = 0 # position cursor at beginning
  while i < (len(t)-2):
    if (t[i][1] - t[i 1][1]) * (t[i 1][1] - t[i 2][1]) >= 0:
      # Same direction: join 2 segments by removing the middlepoint.
      # This test also include the case of an horizontal segment \
      # formed by the first 2 points. We remove the second.
      del( t[i 1])
    else:
      # different directions. Delete nothing. Move cursor by 1
      i  = 1

t1 = [(i,t) for i,t in enumerate(t0)] # add x to every data point
t = t1.copy()      
reduce( t)
graph( t1, t)

Have fun!