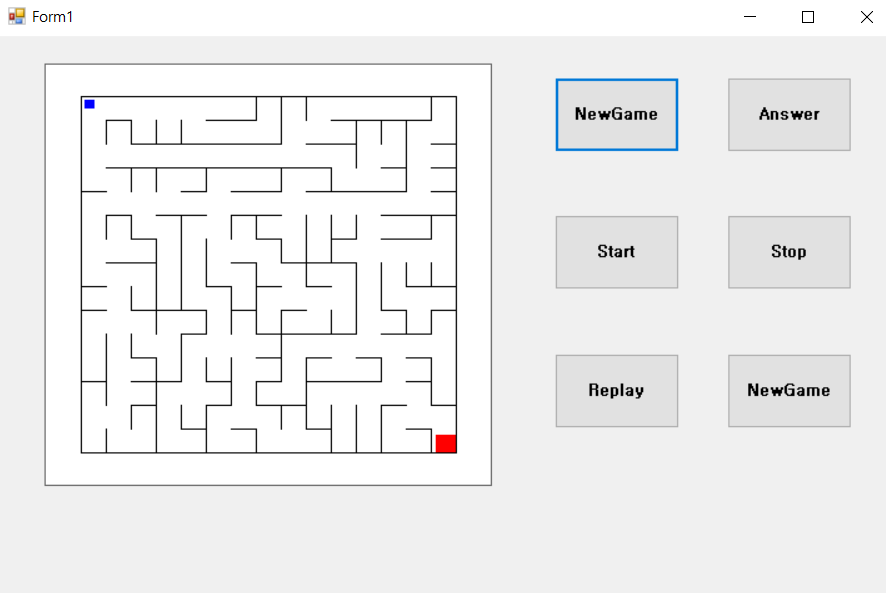
bluepicturebox = PlayerPictureBox
NewgameButton = btnCreate
First, the shape of the maze was implemented in gdi .
How do I implement the function of the player moving, but if I encounter a wall, how do I implement the function of not moving?
private void btnCreate_Click(object sender, EventArgs e)
{
int wid = 15;
int hgt = 15;
CellWidth = picMaze.ClientSize.Width / (wid 2);
CellHeight = picMaze.ClientSize.Height / (hgt 2);
Xmin = (picMaze.ClientSize.Width - wid * CellWidth) / 2;
Ymin = (picMaze.ClientSize.Height - hgt * CellHeight) / 2;
MazeNode[,] nodes = MakeNodes(wid, hgt);
MakeRandomMaze(nodes[0, 0]);
DisplayMaze(nodes);
PlayerPictureBox.Visible = true;
arrivePicturBox.Visible = true;
PlayerPictureBox.Location = new Point(70,51);
}
protected override bool ProcessCmdKey(ref Message msg, Keys keyData)
{
switch (keyData)
{
case Keys.Left:
PlayerPictureBox.Left -= 5;
break;
case Keys.Right:
PlayerPictureBox.Left = 5;
break;
case Keys.Up:
PlayerPictureBox.Top -= 5;
break;
case Keys.Down:
PlayerPictureBox.Top = 5;
break;
default: return base.ProcessCmdKey(ref msg, keyData);
}
return true;
}
CodePudding user response:
You need to implement a collision algorithm between a rectangle (in your case, it is a square) and a line segment. Even though all the shapes are axis-aligned, the algorithm is pretty complex. It involves a lot of vector math and computational geometry tricks. I don't think that you may want to learn the math behind it. Therefore, I don't explain the algorithm. If you want, you can ask another question about how it works.
The implementation is my own implementation. It is not based on any paper on the subject or external example source code. It may not be optimized well. Keep that in mind.
I have created a LineSegment class to hold the line information and if you would use my algorithm, I suggest you to use the class or extend it according to your needs.
PS: I must admit that I supposed that the collision algorithm would be simple but it has evolved a far complex algorithm especially, for a beginner to the collision math.
Here is the example Winforms App. You can tinker it as you want.
using System;
using System.Collections.Generic;
using System.Drawing;
using System.Windows.Forms;
namespace LineRectangleCollision
{
public partial class Form1 : Form
{
public Form1()
{
SetStyle(ControlStyles.AllPaintingInWmPaint | ControlStyles.OptimizedDoubleBuffer | ControlStyles.UserPaint, true);
InitializeComponent();
lineSegments = new List<LineSegment>();
lineSegments.Add(new LineSegment(new PointF(100, 100), new PointF(200, 100)));
lineSegments.Add(new LineSegment(new PointF(100, 100), new PointF(100, 300)));
lineSegments.Add(new LineSegment(new PointF(400, 100), new PointF(400, 300)));
points = new List<PointF>();
points.Add(new PointF(10, 10));
points.Add(new PointF(256, 485));
points.Add(new PointF(110, 50));
rectangle = new RectangleF(0, 0, 30, 30);
}
private List<LineSegment> lineSegments;
private List<PointF> points;
private RectangleF rectangle;
private float velocity = 5f;
protected override void OnPaint(PaintEventArgs e)
{
base.OnPaint(e);
Graphics g = e.Graphics;
g.Clear(Color.White);
for (int i = 0; i < points.Count; i )
g.FillEllipse(Brushes.Blue, points[i].X - 2, points[i].Y - 2, 4, 4);
for (int i = 0; i < lineSegments.Count; i )
lineSegments[i].Draw(g);
g.FillRectangle(Brushes.Red, rectangle);
}
protected override void OnKeyDown(KeyEventArgs e)
{
base.OnKeyDown(e);
switch (e.KeyCode)
{
case Keys.Left:
rectangle.Offset(-velocity, 0);
break;
case Keys.Up:
rectangle.Offset(0, -velocity);
break;
case Keys.Right:
rectangle.Offset(velocity, 0);
break;
case Keys.Down:
rectangle.Offset(0, velocity);
break;
}
bool result = false;
for (int i = 0; i < lineSegments.Count; i )
{
PointF translationVector = CheckCollision(rectangle, lineSegments[i], out result);
if (result)
{
rectangle.Offset(translationVector.X, translationVector.Y);
continue;
}
}
for (int i = 0; i < points.Count; i )
{
PointF translationVector = CheckCollision(rectangle, points[i], out result);
if (result)
{
rectangle.Offset(translationVector.X, translationVector.Y);
continue;
}
}
Invalidate();
}
private PointF CheckCollision(RectangleF rect, LineSegment line, out bool result)
{
PointF lineParallel = line.Unit;
PointF rectCenter = new PointF(rect.X rect.Width / 2.0f, rect.Y rect.Height / 2.0f);
PointF collisionVector = VectorMath.Subtract(rectCenter, line.Start);
float minHalfLength = line.IsVertical ? rect.Width : rect.Height;
minHalfLength /= 2.0f;
float length = VectorMath.Length(VectorMath.Subtract(line.End, line.Start))
float t = VectorMath.Dot(collisionVector, lineParallel);
t = t < 0 ? t minHalfLength : t - minHalfLength;
if (t > 0 && t <= length)
{
PointF translationVector = CheckCollision(rect, line.Start, out result);
if (result)
return translationVector;
translationVector = CheckCollision(rect, line.End, out result);
if (result)
return translationVector;
PointF collisionNormal = VectorMath.RightPerp(lineParallel);
float d = VectorMath.Dot(collisionNormal, collisionVector);
if (d < 0)
collisionNormal = new PointF(-collisionNormal.X, -collisionNormal.Y);
d = Math.Abs(d);
if (d > minHalfLength)
{
result = false;
return PointF.Empty;
}
result = true;
float penetration = minHalfLength - d 0.5f;
return new PointF(penetration * collisionNormal.X, penetration * collisionNormal.Y);
}
result = false;
return PointF.Empty;
}
private PointF CheckCollision(RectangleF rect, PointF point, out bool result)
{
if(rect.Contains(point))
{
LineSegment[] sides = new LineSegment[4];
sides[0] = new LineSegment(rect.X, rect.Y, rect.X rect.Width, rect.Y);
sides[1] = new LineSegment(rect.X rect.Width, rect.Y, rect.X rect.Width, rect.Y rect.Height);
sides[2] = new LineSegment(rect.X rect.Width, rect.Y rect.Height, rect.X, rect.Y rect.Height);
sides[3] = new LineSegment(rect.X, rect.Y rect.Height, rect.X, rect.Y);
result = true;
float minPen = float.MaxValue;
int index = 0;
for (int i = 0; i < 4; i )
{
float d = VectorMath.GetDistanceBetweenPointLine(point, sides[i]);
if (d < minPen)
{
minPen = d;
index = i;
}
}
return VectorMath.Multiply(VectorMath.RightPerp(sides[index].Unit), minPen);
}
result = false;
return PointF.Empty;
}
private class LineSegment
{
public PointF Start;
public PointF End;
public LineSegment(float x0, float y0, float x1, float y1) : this(new PointF(x0, y0), new PointF(x1, y1))
{
}
public LineSegment(PointF start, PointF end)
{
Start = start;
End = end;
}
public bool IsVertical
{
get
{
return Start.X == End.X;
}
}
public PointF Unit
{
get
{
PointF unit = new PointF(End.X - Start.X, End.Y - Start.Y);
float length = VectorMath.Length(unit);
unit.X /= length;
unit.Y /= length;
return unit;
}
}
public void Draw(Graphics g)
{
using (Pen pen = new Pen(Color.Black, 2.0f))
g.DrawLine(pen, Start, End);
}
}
private class VectorMath
{
public static float Dot(PointF v0, PointF v1)
{
return v0.X * v1.X v0.Y * v1.Y;
}
public static float Length(PointF vector)
{
return (float)Math.Sqrt(vector.X * vector.X vector.Y * vector.Y);
}
public static PointF LeftPerp(PointF vector)
{
return new PointF(vector.Y, vector.X);
}
public static PointF RightPerp(PointF vector)
{
return new PointF(-vector.Y, vector.X);
}
public static PointF Add(PointF v0, PointF v1)
{
return new PointF(v0.X v1.X, v0.Y v1.Y);
}
public static PointF Subtract(PointF v0, PointF v1)
{
return new PointF(v0.X - v1.X, v0.Y - v1.Y);
}
public static PointF Multiply(PointF vector, float scaler)
{
return new PointF(vector.X * scaler, vector.Y * scaler);
}
public static PointF Negate(PointF vector)
{
return Multiply(vector, -1.0f);
}
public static float GetDistanceBetweenPointLine(PointF point, LineSegment line)
{
PointF unitParallel = line.Unit;
PointF normal = RightPerp(unitParallel);
float d = Dot(normal, Subtract(point, line.Start));
return Math.Abs(d);
}
}
}
}