Extract curve/surface from an 2-D area of points not equivalently distributed-CodePudding

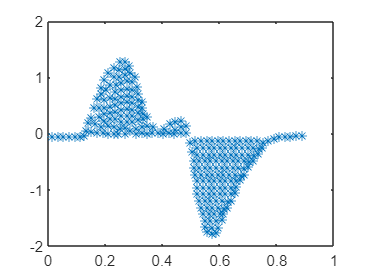
I have data which represents the filled area of two curves. See image. I need to work with the superficial curve (more or less like a sinoidal signal), but I do not see a way to extract only the maximum and minimum points. It is important to know the points are not evenly or equivalently distributed and there isn't a calculated sampling frequency.

This is an example of the data I used to represent the image (my matrix is bigger).

Example = reshape([0.016536 0.036051 0.055566 0.075081 0.094596 0.114111 0.127121 0.134927 0.140131 0.153141 0.153141 0.160947 0.167451 0.172655 0.172655 0.179160 0.180461 0.185665 0.185665 0.188060 0.193797 0.198675 0.198675 0.198675 0.198675 0.198675 0.205180 0.211685 0.212986 0.212986 0.218190 0.218190 0.218190 0.219491 0.219491 0.231200 0.231200 0.232501 0.232501 0.237705 0.237705 0.237705 0.237705 0.237705 0.239331 0.247463 0.250715 0.250715 0.252341 0.252341 0.257220 0.257220 0.257220 0.257220 0.257220 0.257220 0.257220 0.270230 0.270230 0.270230 0.270230 0.270230 0.276735 0.276735 0.276735 0.276735 0.276735 0.276735 0.278361 0.286493 0.289745 0.289745 0.296250 0.296250 0.296250 0.296250 0.296250 0.296250 0.296250 0.306007 0.309260 0.309260 0.312512 0.315765 0.315765 0.315765 0.315765 0.315765 0.328775 0.330401 0.332027 0.332027 0.335280 0.335280 0.348290 0.348290 0.349591 0.366178 0.367805 0.387320 0.403582 0.408461 0.425049 0.427976 0.442612 0.445864 0.447491 0.465379 0.465379 0.465379 0.483268 0.484894 0.496603 0.504409 0.510914 0.510914 0.517419 0.517419 0.523924 0.523924 0.523924 0.523924 0.523924 0.530429 0.530429 0.530429 0.536934 0.536934 0.536934 0.543439 0.543439 0.543439 0.543439 0.543439 0.543439 0.549944 0.549944 0.549944 0.549944 0.549944 0.556449 0.556449 0.556449 0.558075 0.562954 0.562954 0.562954 0.562954 0.562954 0.562954 0.569459 0.569459 0.569459 0.569459 0.575964 0.575964 0.575964 0.575964 0.575964 0.582469 0.582469 0.582469 0.582469 0.582469 0.582469 0.588974 0.588974 0.588974 0.588974 0.588974 0.595479 0.595479 0.595479 0.595479 0.601984 0.601984 0.601984 0.601984 0.601984 0.601984 0.608489 0.608489 0.608489 0.608489 0.614994 0.614994 0.614994 0.616620 0.621499 0.621499 0.621499 0.621499 0.621499 0.628004 0.628004 0.628004 0.629630 0.634509 0.634509 0.641014 0.641014 0.641014 0.641014 0.641014 0.641014 0.647519 0.647519 0.654024 0.654024 0.654024 0.660529 0.660529 0.660529 0.660529 0.667034 0.667034 0.673539 0.673539 0.675165 0.680044 0.680044 0.686549 0.686549 0.688175 0.693053 0.699558 0.699558 0.699558 0.706063 0.712568 0.719073 0.719073 0.720700 0.732083 0.735336 0.740215 0.751598 0.753225 0.771113 0.790628 0.810143 0.829658 0.849173 0.868688 0.888203 -0.053191 -0.053191 -0.053191 -0.053191 -0.053191 -0.046647 -0.033559 0.044970 0.195483 0.290372 0.035154 0.457245 0.182395 0.624118 0.018794 0.300188 0.457245 0.705918 0.133315 0.810811 0.015522 0.957864 0.604486 0.470333 0.352540 0.234747 0.781175 0.005706 1.085473 0.143131 0.483421 0.365628 0.260923 0.873446 0.637860 1.020033 -0.007382 1.179707 0.119572 0.745183 0.627390 0.509597 0.391804 0.274012 0.879336 0.005706 1.137825 1.020033 1.271978 0.094050 0.902240 0.784447 0.666654 0.548861 0.431069 0.313276 0.221659 1.281794 1.164002 1.046209 0.103866 0.005706 0.797535 0.679742 0.561949 0.444157 0.326364 0.208571 0.938232 1.203266 1.085473 0.054786 0.918600 0.784447 0.666654 0.548861 0.431069 0.313276 0.221659 1.006944 0.094050 0.005706 0.830255 0.719007 0.601214 0.483421 0.365628 0.247835 0.012250 0.133315 0.575038 0.457245 0.352540 0.260923 0.005706 0.300188 0.143131 0.015522 0.130043 0.025338 0.005706 0.094050 0.021411 0.172579 0.005706 0.077690 0.211843 0.234747 0.116954 0.012250 0.015522 0.143131 -0.155278 -0.328041 -0.485098 -0.596346 -0.131719 -0.720683 -0.249512 -0.367305 -0.838476 -0.956269 -1.067518 -0.485098 -0.602890 -1.191854 -0.131719 -0.720683 -1.309647 -0.249512 -0.367305 -0.838476 -0.956269 -1.074062 -1.427440 -0.485098 -0.602890 -1.191854 -1.545233 -1.656481 -0.131719 -0.720683 -1.309647 -1.741554 -0.249512 -0.367305 -0.838476 -0.956269 -1.074062 -1.427440 -0.485098 -0.602890 -1.191854 -1.545233 -0.131719 -0.720683 -1.309647 -1.663026 -1.780818 -0.249512 -0.367305 -0.838476 -0.956269 -1.074062 -1.427440 -0.485098 -0.602890 -1.191854 -1.545233 -1.761186 -0.131719 -0.720683 -1.309647 -1.672842 -0.249512 -0.367305 -0.838476 -0.956269 -1.074062 -1.427440 -0.485098 -0.602890 -1.191854 -1.532145 -0.131719 -0.720683 -1.427440 -1.329279 -0.249512 -0.367305 -0.838476 -0.956269 -1.074062 -0.485098 -0.602890 -1.309647 -1.211486 -0.131719 -0.720683 -0.249512 -0.367305 -0.838476 -0.956269 -1.074062 -1.191854 -0.485098 -0.602890 -0.131719 -0.720683 -1.054429 -0.249512 -0.367305 -0.838476 -0.949725 -0.485098 -0.602890 -0.131719 -0.818844 -0.740315 -0.249512 -0.367305 -0.485098 -0.720683 -0.622523 -0.131719 -0.249512 -0.367305 -0.583258 -0.504730 -0.131719 -0.249512 -0.485098 -0.386937 -0.131719 -0.357489 -0.269144 -0.249512 -0.151351 -0.125175 -0.085911 -0.059735 -0.053191 -0.053191 -0.033559 -0.033559 ],[245    2]);

I will appreciate any hint to a function I can use or a method. I tried with some functions like mesh or findpeaks but didn't work.

CodePudding user response：

You could try using the movmax function. Signal processing experts may well have a better way, but here's my attempt:

% First compute the moving maximum of the absolute value
movMaxAbs = movmax(abs(Example(:,2)),10);
% To correct the sign, we need something like this
signCorrection = sign(smoothdata(Example(:,2)));
plot(Example(:,1), Example(:,2), Example(:,1), movMaxAbs .* signCorrection);