How to decide which feature in model can be deleted (feature selection)?-CodePudding

I'm new to Machine Learning, and I'm working on dataset "Combined Cycle Power Plant over 6 years (2006-2011)", when the power plant was set to work with full load. Features consist of hourly average ambient variables Temperature (AT), Ambient Pressure (AP), Relative Humidity (RH) and Exhaust Vacuum (V) to predict the net hourly electrical energy output (PE) of the plant.

And this is my output:

How I can decide to remove 1 feature that may not be as important as the other ones for prediction. (since the data has been normalized, may be done by looking at the weights of each feature in the learned model.)
The Linear Regression coefficients (weight) of columns (features - 'AT', 'V', 'AP', 'RH', 'PE') which I calculated with numpy.linalg.lstsq is:

[ 4.54458108e 02 -1.44125679e 01 -3.11527582e 00  3.78157228e-01 -2.06364959e 00]

In this case, I guess I can choose the third one which is 'AP' to remove from features. Is that correct?

CodePudding user response：

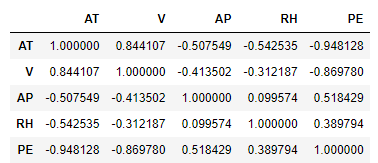
If your question is about deleting features and not losing performance, I suggest you check the correlation between your data points.

You could use the correlation pandas already has built in.

corr_matrix = df.corr()
corr_matrix[['AT', 'AP', 'RH', 'V']]

And see the output. For any two features X and Y, if they are tightly correlated, then it is not wise to use both of them. You can easily remove any one. Alternatively, you can combine the two features and label them as Z = XY and use them as one feature.

The correlation matrix is as follows

# using all the attributes
X = df.drop(['PE', 'RH'], axis=1)
y = df['PE']

lr = LinearRegression()

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=27)
lr.fit(X_train, y_train)
lr.predict(X_test)
print(lr.score(X_test, y_test))

>>> 0.9297044622422397

Now removing RH (since it has the least correlation)

X = df.drop(['PE', 'RH'], axis=1)
y = df['PE']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=27)
lr.fit(X_train, y_train)
lr.predict(X_test)
print(lr.score(X_test, y_test))

>>> 0.9175575321043363

I suggest you remove RH and see how the model performs.