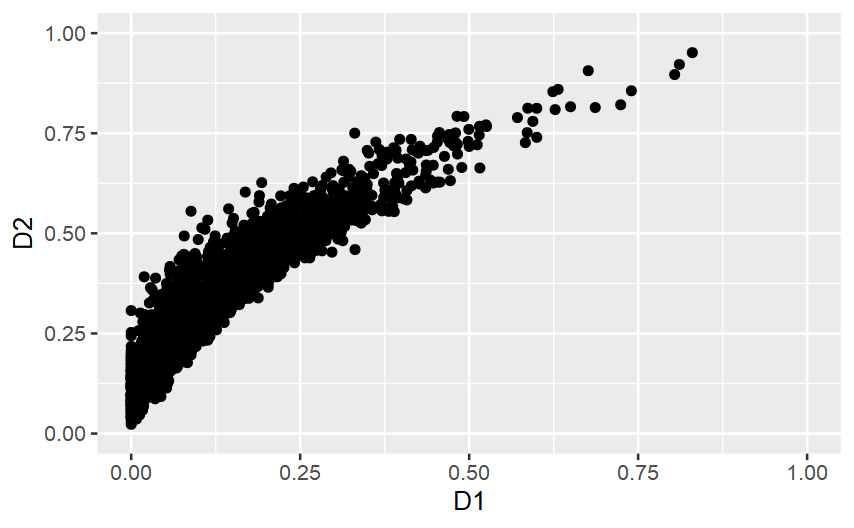
I have a tibble with two columns, D1 and D2. These are distributed as the figure.

I want to split the obs. in 2 clusters. The theory predicts that one of the two will be much smaller than the other. To me, given the liner relation (R^2 = .9) between the two dimensions, a reasonable split is kinda D1 > 75, or kinda D1 > .55. However, when I run a kmean(2) on the data, the suggested clusters are much more balanced.

I need an algorithm that spots that the clusters must be not balanced, and instead maximising the distance between clusters. I was thinking about the distance between the cluster averages of the linear predicted values or, even more simply, just the distance in cluster averages of the harmonic mean of D1 and D2

Any other suggestions? I looked for Linear Discriminant Analysis (MASS:lda()) but it seems a supervised model, which is not helpful here.

CodePudding user response：

Please reference to https://scikit-learn.org/stable/modules/clustering.html if you want to check different clustering methods for different data distributions.

For your case I will try with Gaussian Mixture or DBSCAN.