Plotting the basic reproduction number against two parameters-CodePudding

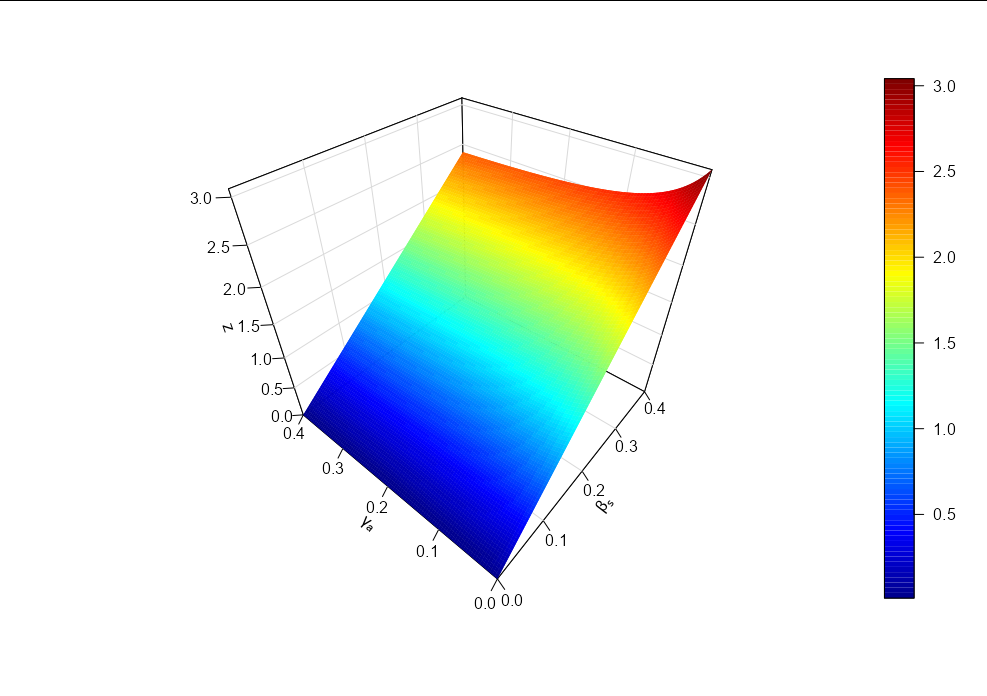
I am trying to replicate the following graph from the paper,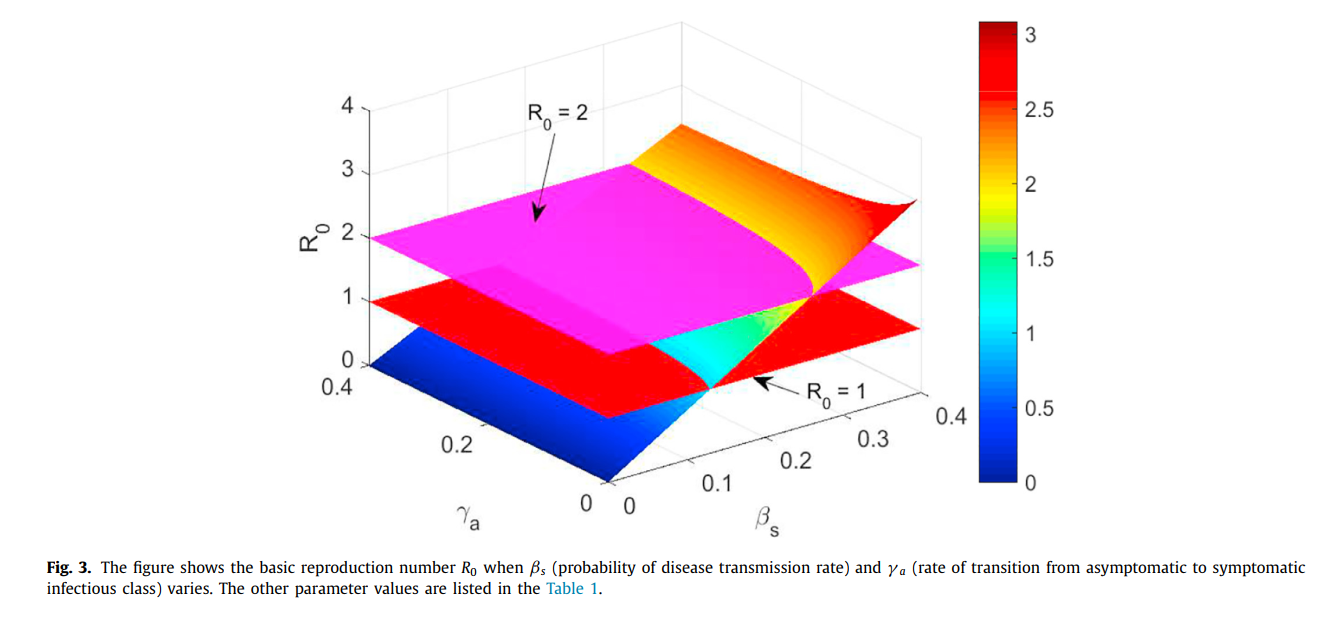

Given below are the parameter values and the formula for the basic reproductive number.

beta_s = 0.274
alpha_a = 0.4775
alpha_u = 0.695
mu = 0.062
gamma_a = 0.29
q_i = 0.078
1/eta_i = 0.009
1/eta_u = 0.05


R_0 = (beta_s*alpha_a)/(gamma_a mu)   (beta_s*alpha_u*gamma_a*(1-q_i))/((gamma_a mu) 
(eta_u mu))

I would be very much thankful, if someone could help me draw the graph using R or MATLAB. Thanks a lot in advance!

CodePudding user response：

Adding to @AlanCameron's answer to add horizontal planes:

## previous code
perspbox(beta, gamma, z = R, theta = -50, ticktype = "detailed",
         col.grid = "gray85", bty = "u",
         xlab = "\u03b2\u209b", ylab = "\u03b3\u2090")

pp <- persp3D(beta, gamma, z = R, theta = -50, add = TRUE)

Horizontal plane-adding function:

plane3D <- function(z, 
              col = adjustcolor("blue", alpha.f = 0.2),
              border = NA,
              xlim = c(0,0.4), ylim = c(0, 0.4)) {
   dd <- expand.grid(x=xlim, y = ylim, z= z)
   rr <- with(dd, trans3D(x,y,z,pp))
   perm <- c(1,3,4,2)
   polygon(rr$x[perm], rr$y[perm], col = col, border = border)
}

Add planes:

plane3D(1)
plane3D(2, col = adjustcolor("red", alpha.f = 0.2))

It's also pretty easy to do the basics of this with the rgl package, which also allows dynamic rotation and handles occlusion properly:

library(rgl)
persp3d(beta, gamma, R, theta = -50, col = "gray")
## horizontal plane at z = Z →
##    0*x   0*y   1*z - Z = 0
##  a = 0, b = 0, c = 1, d = -Z 
planes3d(0, 0, 1, -1, col = "red")
planes3d(0, 0, 1, -2, col = "blue")

Decorating (color gradient on surface etc.) is a little harder.

CodePudding user response：

In R, you could use the plot3D library:

library(plot3D)

R_0 <- function(beta_s, gamma_a, alpha_a = 0.4775, alpha_u = 0.695,
                mu = 0.062, q_i = 0.078, eta_i = 0.009, eta_u = 0.05) {
  
  A <- beta_s * alpha_a / (gamma_a   mu) 
  B <- beta_s * alpha_u * gamma_a * (1 - q_i) / ((gamma_a   mu) * (eta_u   mu))
  A   B
}

beta <- gamma <- seq(0, 0.4, length.out = 100)

R <- outer(beta, gamma, R_0)

perspbox(beta, gamma, z = R, theta = -50, ticktype = "detailed",
         col.grid = "gray85", bty = "u",
         xlab = "\u03b2\u209b", ylab = "\u03b3\u2090")

persp3D(beta, gamma, z = R, theta = -50, add = TRUE)