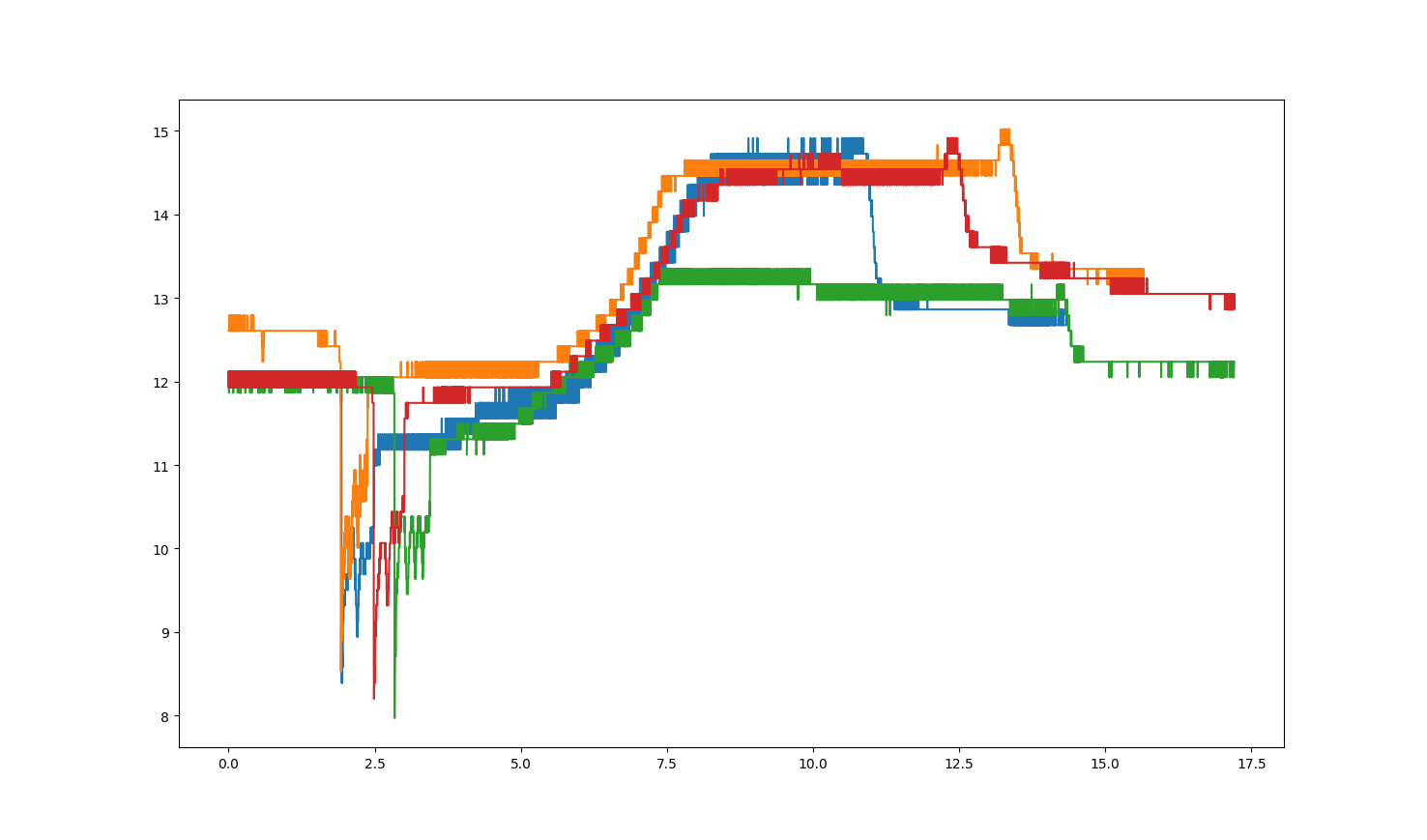
I want to overlay some graphs out of CSV data (two datasets). The graph I got from my dataset is shown down below.
Is there any way to plot those datasets over specific points? I would like to overlay these plots by using the anchor of the "big drop" to compare them in a better way.
The code used:
import pandas as pd
import matplotlib.pyplot as plt
# Read the data
data1 = pd.read_csv('data1.csv', delimiter=";", decimal=",")
data2 = pd.read_csv('data2.csv', delimiter=";", decimal=",")
data3 = pd.read_csv('data3.csv', delimiter=";", decimal=",")
data4 = pd.read_csv('data4.csv', delimiter=";", decimal=",")
# Plot the data
plt.plot(data1['Zeit'], data1['Kanal A'])
plt.plot(data2['Zeit'], data2['Kanal A'])
plt.plot(data3['Zeit'], data3['Kanal A'])
plt.plot(data4['Zeit'], data4['Kanal A'])
plt.show()
plt.close()
I would like to share you some data here:
CodePudding user response:
Part 1: Anchor times
A simple way is to find the times of interest (lowest point) in each frame, then plot each series with x=t - t_peak instead of x=t. Two ways come to mind to find the desired anchor points:
- Simply using the global minimum (in your plots, that would work fine), or
- Using the most prominent local minimum, either from first principles, or using scipy's
find_peaks().
But first of all, let us attempt to build a reproducible example:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def make_sample(t_peak, tmax_approx=17.5, n=100):
# uneven times
t = np.random.uniform(0, 2*tmax_approx/n, n).cumsum()
y = -1 / (0.1 2 * np.abs(t - t_peak))
trend = 4 * np.random.uniform(-1, 1) / n
level = np.random.uniform(10, 12)
y = np.random.normal(trend, 1/n, n).cumsum() level
return pd.DataFrame({'t': t, 'y': y})
poi = [2, 2.48, 2.6, 2.1]
np.random.seed(0)
frames = [make_sample(t_peak) for t_peak in poi]
plt.rcParams['figure.figsize'] = (6,2)
fig, ax = plt.subplots()
for df in frames:
ax.plot(*df.values.T)
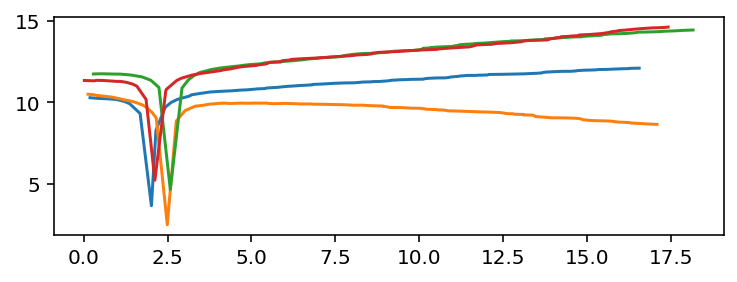
In this case, we made the problem maximally inconvenient by giving each time series its own, independent, unevenly distributed time sampling.
Now, retrieving the "maximum drop" by global minimum:
peaks = [df.loc[df['y'].idxmin(), 't'] for df in frames]
>>> peaks
[2.0209774600118764, 2.4932468358014157, 2.5835972003585472, 2.12438578790615]
fig, ax = plt.subplots()
for t_peak, df in zip(peaks, frames):
ax.plot(df['t'] - t_peak, df['y'])
But imagine a case where the global minimum is not suitable. For example, add a large sine wave to each series:
frames = [df.assign(y=df['y'] 5 * np.sin(df['t'])) for df in frames]
# just plotting the first series
df = frames[0]
plt.plot(*df.values.T)
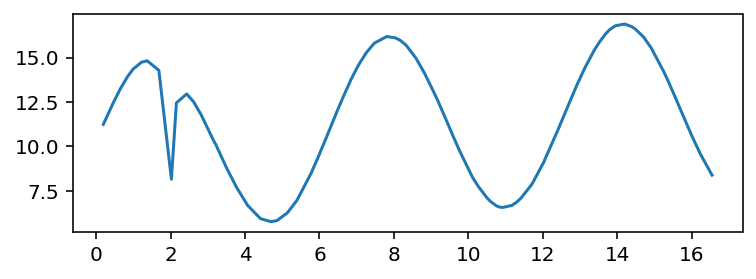
Clearly, there are several local minima, and the one we want ("sharpest drop") is not the global one.
A simple way to find the desired sharpest drop time is by looking at the difference from each point to its two neighbors:
def arg_steepest_min(v):
# simply find the minimum that is most separated from the surrounding points
diff = np.diff(v)
i = np.argmin(diff[:-1] - diff[1:]) 1
return i
peaks = [df['t'].iloc[arg_steepest_min(df['y'])] for df in frames]
>>> peaks
[2.0209774600118764, 2.4932468358014157, 2.5835972003585472, 2.12438578790615]
# just plotting the first curve and the peak found
df = frames[0]
plt.plot(*df.values.T)
plt.plot(*df.iloc[arg_steepest_min(df['y'])].T, 'x')
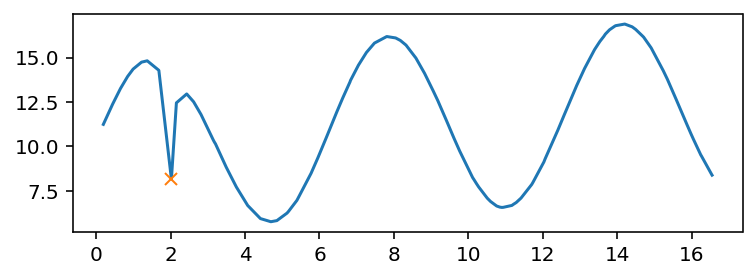
There are more complex cases where you want to bring the full power of find_peaks(). Here is an example that uses the most prominent minimum, using a certain number of samples for neighborhood:
from scipy.signal import find_peaks, peak_prominences
def arg_most_prominent_min(v, prominence=1, wlen=10):
peaks, details = find_peaks(-v, prominence=prominence, wlen=wlen)
i = peaks[np.argmax(details['prominences'])]
return i
peaks = [df['t'].iloc[arg_most_prominent_min(df['y'])] for df in frames]
>>> peaks
[2.0209774600118764, 2.4932468358014157, 2.5835972003585472, 2.12438578790615]
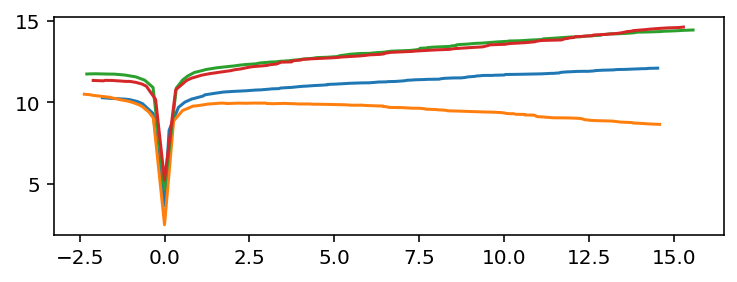
In this case, the peaks found by both methods are the same. Aligning the curves gives:
fig, ax = plt.subplots()
for t_peak, df in zip(peaks, frames):
ax.plot(df['t'] - t_peak, df['y'])
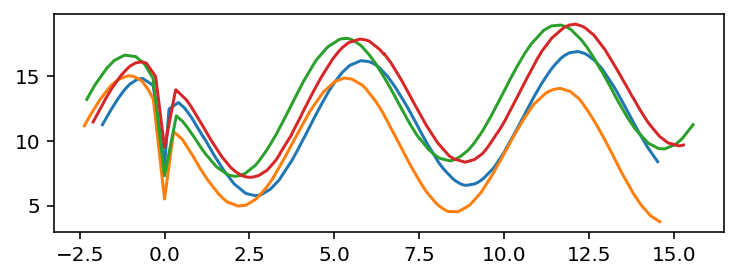
Part 2: aligning the time series for numeric operations
Having found the anchor times and plotted the time series by shifting the x-axis accordingly, suppose now that we want to align all the time series, for example to somehow compare them to one another (e.g.: differences, correlation, etc.). In this example we made up, the time samples are not equidistant and all series have their own sampling.
We can use resample() to achieve our goal. Let us convert the frames into actual time series, transforming the column t (supposed in seconds) into a DateTimeIndex, after shifting the time using the previously found t_peak and using an arbitrary "0" date:
frames = [
pd.Series(
df['y'].values,
index=pd.Timestamp(0) (df['t'] - t_peak) * pd.Timedelta(1, 's')
) for t_peak, df in zip(peaks, frames)]
>>> frames[0]
t
1969-12-31 23:59:58.171107267 11.244308
1969-12-31 23:59:58.421423545 12.387291
1969-12-31 23:59:58.632390727 13.268186
1969-12-31 23:59:58.823099841 13.942224
1969-12-31 23:59:58.971379021 14.359900
...
1970-01-01 00:00:14.022717327 10.422229
1970-01-01 00:00:14.227996854 9.504693
1970-01-01 00:00:14.235034496 9.489011
1970-01-01 00:00:14.525163506 8.388377
1970-01-01 00:00:14.526806922 8.383366
Length: 100, dtype: float64
At this point, the sampling is still uneven, so we use resample to get a fixed frequency. One strategy is to oversample and interpolate:
frames = [df.resample('100ms').mean().interpolate() for df in frames]
for df in frames:
df.plot()
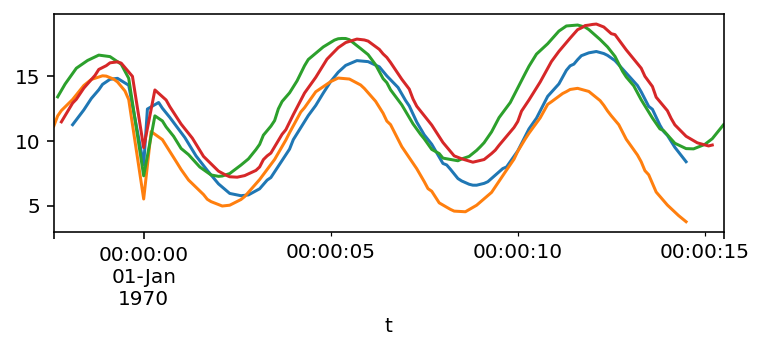
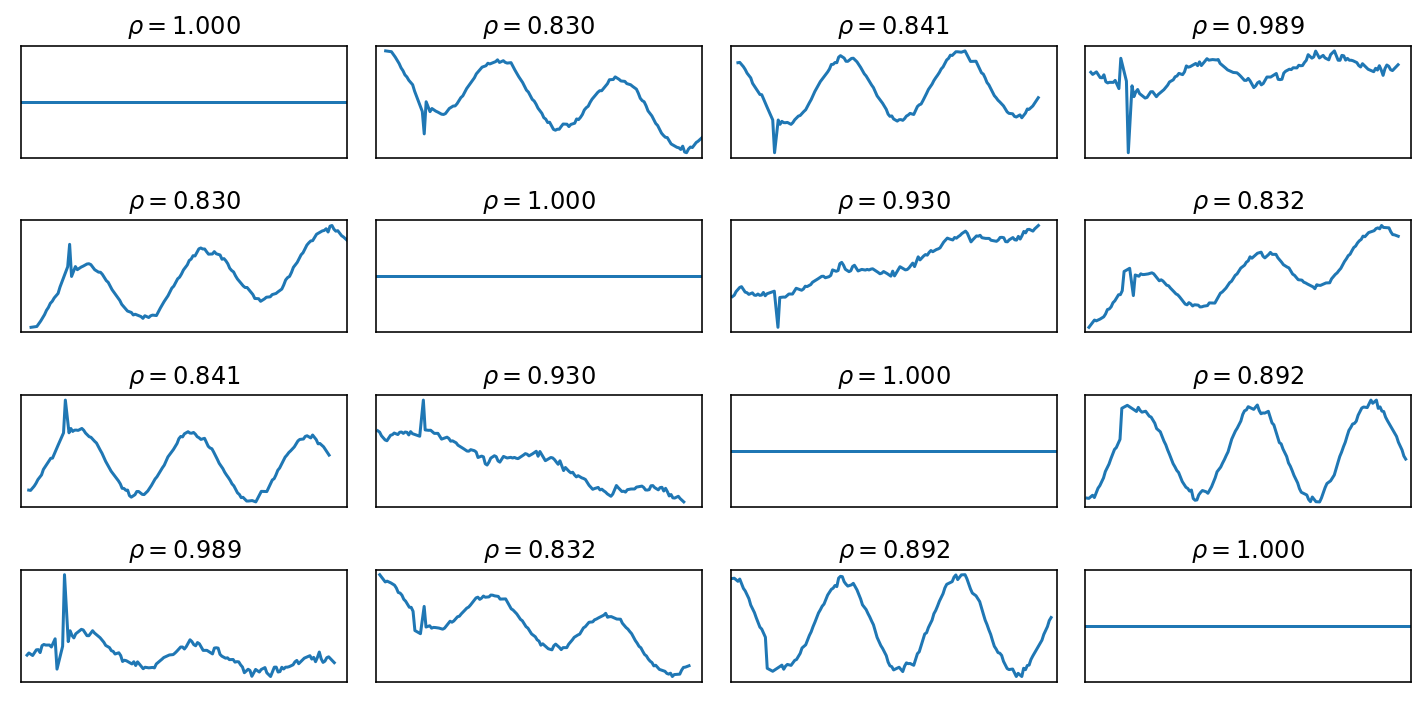
At this point, we can compare the Series. Here are the pairwise differences and correlations:
fig, axes = plt.subplots(nrows=len(frames), ncols=len(frames), figsize=(10, 5))
for axrow, a in zip(axes, frames):
for ax, b in zip(axrow, frames):
(b-a).plot(ax=ax)
ax.set_title(fr'$\rho = {b.corr(a):.3f}$')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.tight_layout()