Probability density function with triangular distribution of parameters-CodePudding

How do you compute this probability density function, with a triangular distribution of parameters (a,b,c)?

f(x)= 0 , x<a
      2(x-a)/((b-a)(c-a)) , a <= x <= c
      2(b-x)/((b-a)(b-c)) , c < x <=b
      0 , x> b

CodePudding user response：

Expanding on @StéphaneLaurent‘s comments, you can define a piecewise function using a series of ifelse() calls (or dplyr::case_when()).

f <- function(x, A, B, C) {
  out <- ifelse(
    x < A | B < x,
    0,
    ifelse(
      A <= x & x <= C,
      (2*(x-A))/((B-A)*(C-A)),
      ifelse(
        C < x & x <= B,
        (2*(B-x))/((B-A)*(B-C)),
        NA_real_
  )))
  if (any((is.na(out) | is.nan(out)) & (!is.na(x) & !is.nan(x)))) {
    warning("f(x) undefined for some input values")
  }
  out
}

Taking it for a spin:

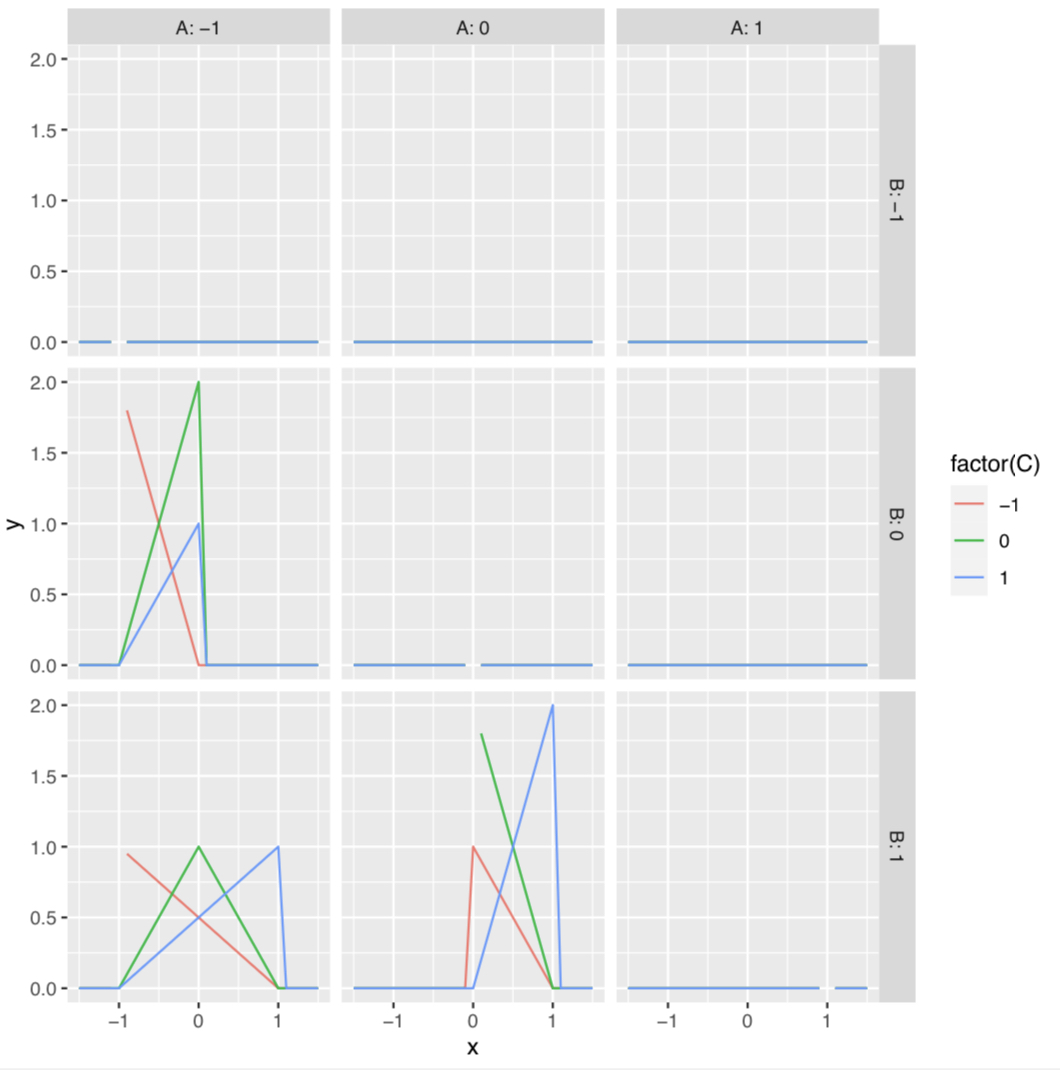
library(ggplot2) 
dat <- expand.grid(
  x = seq(-1.5, 1.5, by = 0.1),
  A = -1:1,
  B = -1:1,
  C = -1:1
)

dat$y <- with(dat, f(x, A, B, C))
# Warning message:
# In f(x, A, B, C) : f(x) undefined for some input values

ggplot(dat, aes(x, y))  
  geom_line(aes(color = factor(C)))  
  facet_grid(B ~ A, labeller = label_both)

CodePudding user response：

Here is an option for a density function and a random function.

dtri <- function(x, A, B, C) {
  n <- length(x)
  i <- 1:n
  if (length(A) == 1) A <- rep(A, n)
  if (length(B) == 1) B <- rep(B, n)
  if (length(C) == 1) C <- rep(C, n)
  abc <- Rfast::rowSort(matrix(c(A, B, C), n, 3))
  bln <- x < abc[,2]
  p <- 2*abs(x - abc[i   2*n*!bln])/(abc[,3] - abc[,1])/(abc[i   n*(2 - bln)] - abc[i   n*(1 - bln)])
  p[x < abc[,1] | x > abc[,3]] <- 0
  p
}

rtri <- function(n, a, b, c) {
  if (a > b) {a <- (b - a)   (b <- a)}
  if (b > c) {c <- (b - c)   (b <- c)}
  fb <- (b - a)/(c - a)
  U <- runif(n)
  blna <- U < fb
  r <-numeric(n)
  r[blna] <- a   sqrt(U[blna]*(c - a)*(b - a))
  r[!blna] <- c - sqrt((1 - U[!blna])*(c - a)*(c - b))
  r
}