Prove the central limit theorem with a sum when n increases-CodePudding

I'm trying to use Monte Carlo simulation in order to show how the sum of an uniform sample is normal distributed when the dimension of the sample increase.

More precisely: let define $X ~ U[2,3]$ where $X_1,...,X_n$ is an iid sample from X and $S = \sum_{1}^{n}(X_i). I want use Monte Carlo Simulation in order to show that the distribution of S is approximately normal when n is large (as predicted by Central Limit Theorem).

What I want to show is that when the number of observation in S rise its distribution is more normal. Is also important that I'm talking about the sum of $X_i$, so I'm not considering the general case with the mean.

The problem is that I can obtain a more (or less) normal distribution when I increase (or decrease) the number of time in the Monte Carlo. instead, If I change the sample dimension the differences are VERY low, I can see a normal distribution even when the sample is 10 and, for example, from 10 to 100 i can't notice any significant difference.

Here there is my MWE:

    #create random variable with sample size of 1000 that is uniformally distributed
    data <- runif(n=10000, min=2, max=3)
    hist(data, col='steelblue', main='Histogram from the Uniform')

    #I take, for 1000 times, the sum of a sample=10 from X
    sample10 <- c()
    n = 1000
    for (i in 1:n){
     sample10[i] = sum(sample(data, 10, replace=TRUE))
    }
    hist(sample10, col ='steelblue', main='Sample size = 10', prob=TRUE)
    qqnorm(sample10); qqline(sample10)


    #Increasing the sample dimension
    sample100 <- c()
    n = 1000
    for (i in 1:n){
     sample100[i] = sum(sample(data, 100, replace=TRUE))
    }
    hist(sample100, col ='steelblue', main='Sample size = 100', prob=TRUE)
    qqnorm(sample100); qqline(sample100)

What am I doing wrong?

PS. Sorry for my English, any request for clarification is welcome.

CodePudding user response：

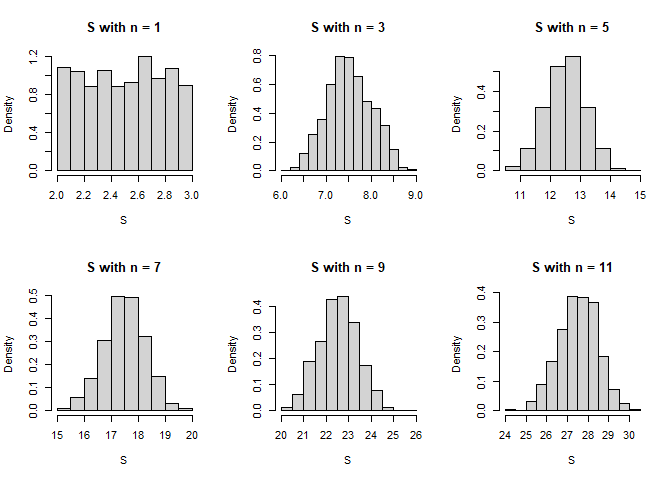
Here is a simulation of the sums of n random uniforms U(2, 3) with n varying from 1 to 11 by steps of 2. Each sum is replicated 1000 times.

set.seed(2022)

nvec <- seq(1, 12, by = 2)
R <- 1e3
S_list <- lapply(nvec, \(n) {
  replicate(R, sum(runif(n, 2, 3)))
})

^{Created on 2022-12-01 with reprex v2.0.2}

Now the histograms. You will see that convergence is very quick. That feature is even the basis of a CLT-based pseudo-RNG algorithm for the standard normal.

old_par <- par(mfrow = c(2, 3))
mapply(\(S, n) {
  main <- sprintf("S with n = %d", n)
  hist(S, main = main, freq = FALSE)
  invisible(NULL)
}, S_list, nvec)

#> [[1]]
#> NULL
#> 
#> [[2]]
#> NULL
#> 
#> [[3]]
#> NULL
#> 
#> [[4]]
#> NULL
#> 
#> [[5]]
#> NULL
#> 
#> [[6]]
#> NULL
par(old_par)

^{Created on 2022-12-01 with reprex v2.0.2}

Don't worry about these NULL's, they are the return value of mapply.

And the QQ-plots.

old_par <- par(mfrow = c(2, 3))
mapply(\(S, n) {
  main <- sprintf("S with n = %d", n)
  qqnorm(S, main = main)
  qqline(S)
}, S_list, nvec)

#> [[1]]
#> NULL
#> 
#> [[2]]
#> NULL
#> 
#> [[3]]
#> NULL
#> 
#> [[4]]
#> NULL
#> 
#> [[5]]
#> NULL
#> 
#> [[6]]
#> NULL
par(old_par)

^{Created on 2022-12-01 with reprex v2.0.2}