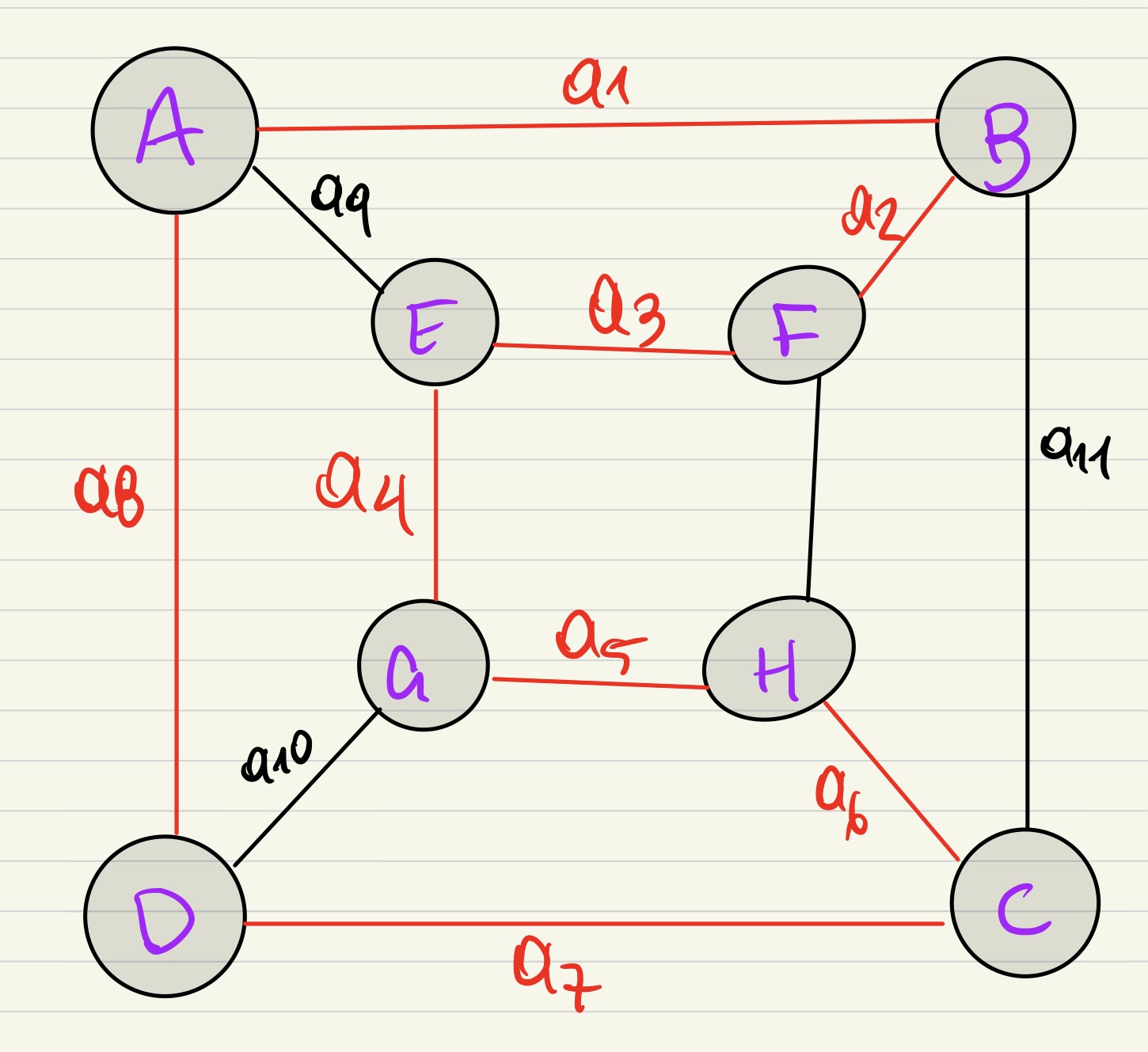
I have the following undirected graph (picture) that contains a cycle or a Hamiltonian path of length |V|= 8. The cycle (path) with no repeated edges and vertices is the red line. The adjacency matrix is :
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| B | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| C | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| D | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| E | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| F | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| G | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| H | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
How can I plot this graph in R ?
Ham = matrix(c(0,1,0,1,1,0,0,0,
1,0,1,0,0,1,0,0,
0,1,0,1,0,0,0,1,
1,0,1,0,0,0,1,0,
1,0,0,0,0,1,1,0,
0,1,0,0,1,0,0,1,
0,0,0,1,1,0,0,1,
0,0,1,0,0,1,1,0),8,8)
Ham
CodePudding user response:
Update
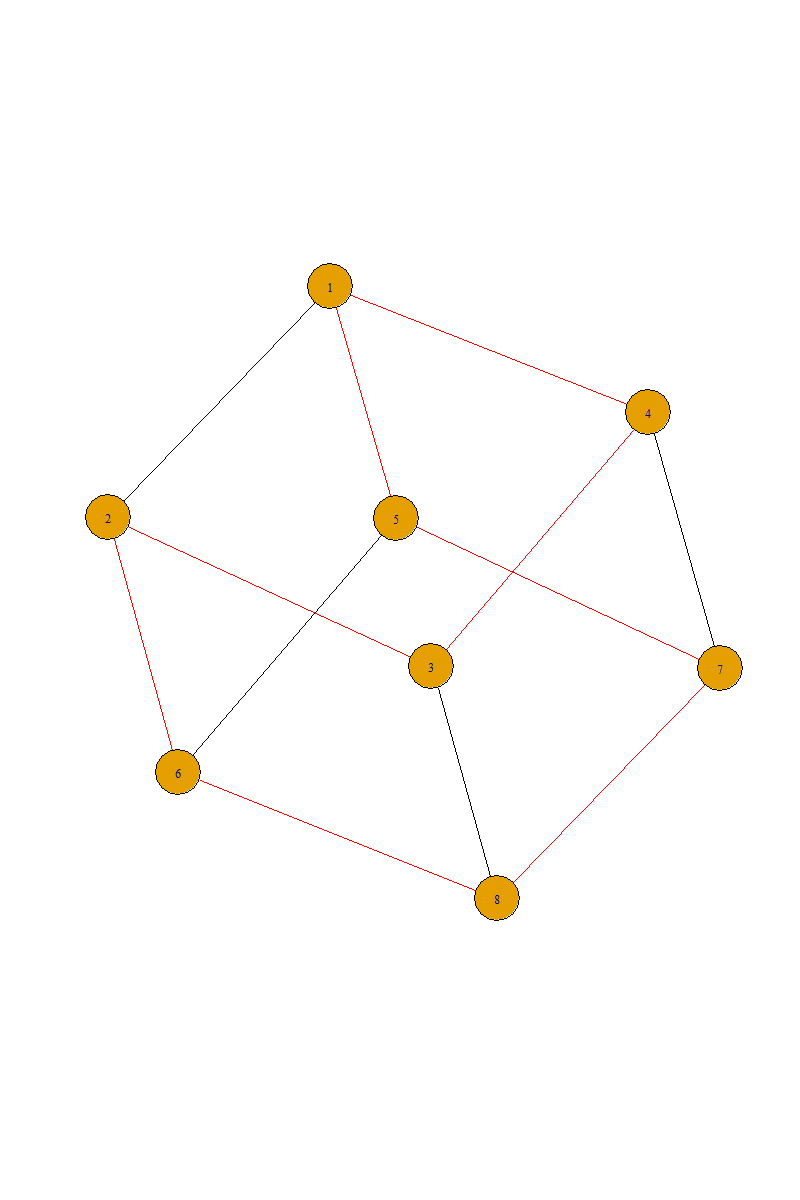
If you need only one of all the Hamilton circles, you can try graph.subisomorphic.lad (thanks for the advice from @Szabolcs), which speeds up a lot if you don't need to list out all the possibilities, e.g.,
g <- graph_from_adjacency_matrix(Ham, "undirected")
es <- graph.subisomorphic.lad(make_ring(vcount(g)), g)$map
g %>%
set_edge_attr("color", value = "black") %>%
set_edge_attr("color",
get.edge.ids(g, c(rbind(es, c(es[-1], es[1])))),
value = "red"
) %>%
plot()
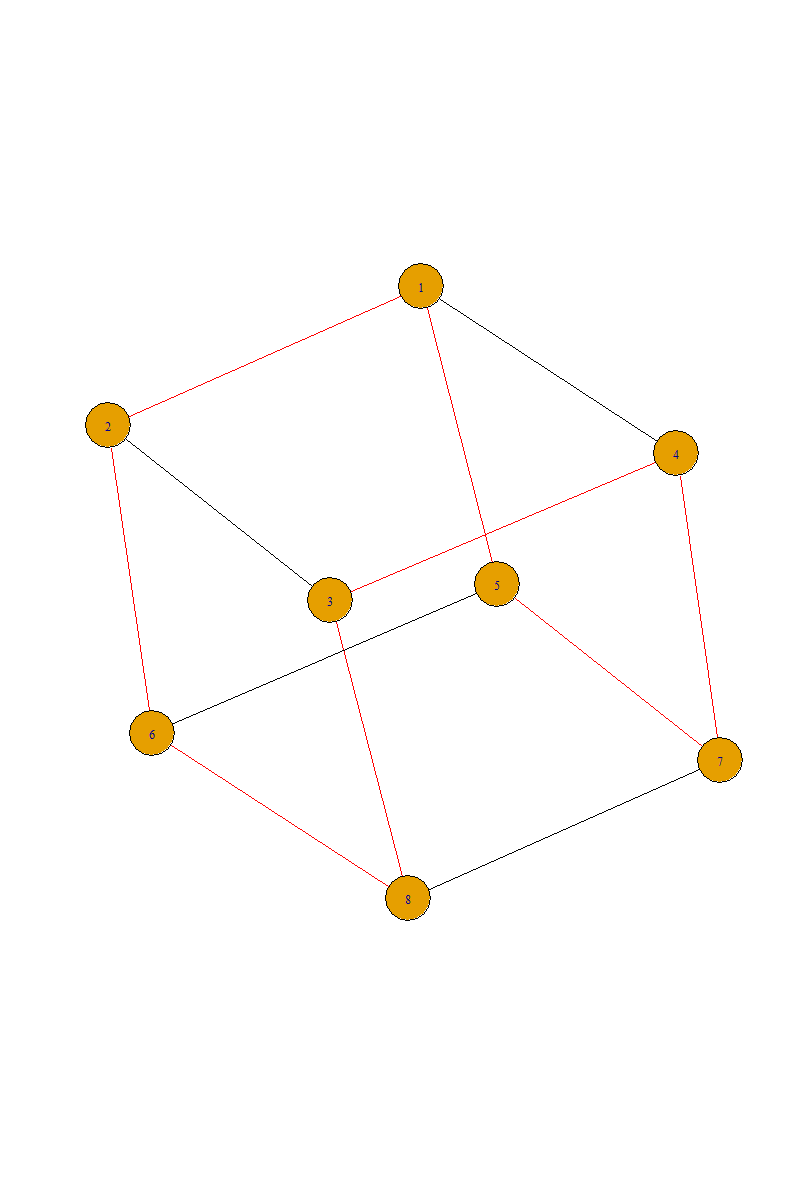
If you want to find all Hamilton circles:
You should be aware of the fact that the Hamilton circle is isomorphic to a ring consisting of all vertices, so we can resort to subgraph_isomorphisms to find out all those kinds of "rings", e.g.,
g <- graph_from_adjacency_matrix(Ham, "undirected")
lst <- lapply(
subgraph_isomorphisms(make_ring(vcount(g)), g),
function(es) {
g %>%
set_edge_attr("color", value = "black") %>%
set_edge_attr("color",
get.edge.ids(g, c(rbind(es, c(es[-1], es[1])))),
value = "red"
)
}
)
where lst is a list of graphs, and you can see
and so on so forth.