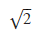Exact value of a root on Python-CodePudding

I'm writing a programme that converts complex numbers. Right now I'm having problems with this piece of code:

import numpy

complexnr = 1 1j
mod= numpy.absolute(complexnr)
print(mod)

The output of this code is:

1.4142135623730951

I would like to get √2 as the output.

I have been advised to use the sympy module but I have had no luck with this either. What would be the easiest way to get this result?

CodePudding user response：

Works by using

I (from sympy) rather than 1j
builtin abs function which calls sympby.Abs for complex arguments

Code

from sympy import I

complexnr = 1   I       # use I rather than 1j
print(abs(complexnr))   # also works with np.abs and np.absolute

Output

CodePudding user response：

If you want to use SymPy, you have to write the complex numbers as sympy expressions.

from sympy import *
cabs = lambda z: sqrt(re(z)**2   im(z)**2)
complexnr = 1   1j
print(cabs(complexnr))
# out: 1.4142135623731

We are getting a float number because complexnr is of type complex and its real and imaginary parts are of type float. Thus, SymPy's re and im functions returns float numbers. But when sqrt receives a float number, it evaluates the result.

We can workaround this problem in two ways.

The first: if we are dealing with simple complex numbers where real and imaginary parts are integers, we can write the complex number as a string, sympify it (which means convert to a sympy expression):

complexnr = sympify("1   1j")
print(cabs(complexnr))
# out: sqrt(2)

A second way consist in using the complex number directly, then apply nsimplify in order to attempt to convert the resulting float number to some symbolic form:

complexnr = 1   1j
result = cabs(complexnr) # result is a Float number, 1.4142135623731
print(result.nsimplify())
# out: sqrt(2)