How to add text combined with indicators (R2, RSME and n) to a plot or to ggplot?-CodePudding

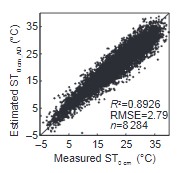
I need to make a graph of actual vs. predicted in a plot exactly like the image, but it exceeds my r skill.

I have R2, RMSE and n calculated as independent objects. I have tried standard plot with 'text()' and ggplot with 'geom_tex()' I can't get close to what I want.

How do I combine text with the objects?

How can I position them same as in the plot, with a new line for each indicator?

Can I make my axes have the same proportion to get a square plot?

CodePudding user response：

The following will present a solution for a baseR-plot and a ggplot. I have created an artificial DF which can be found at the end of the post.

At first a linear model is made which is later used for both plots to create the labels.

To your first question how to combine text with objects from this model(like R^2, RSME) you may refer to the create labels part.

The position for Base R-plot is defined in text(x,y,..) where x and y give the position of this text element.

For ggplot the label position is defined in annotate(x, y, ...).

One way to make the plot square in Base R is to define par(pty="s").

For ggplot you can define the aspect.ratio in theme.

linear Fit


model <- lm(y~x, data = df)
ss <- summary(model)

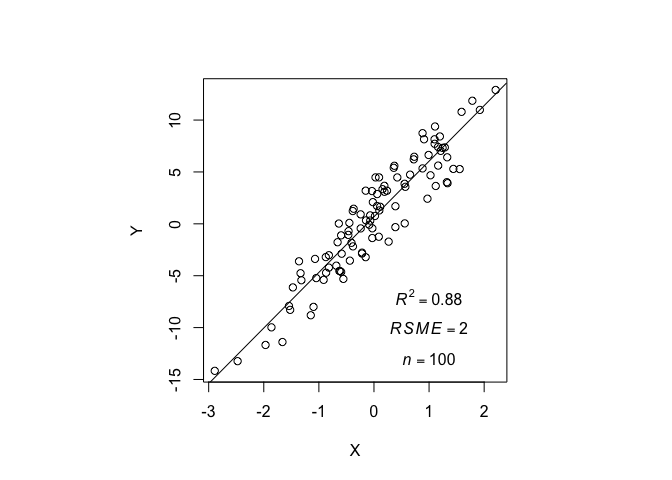
BASE R-Plot

## create labels
R_label = bquote(italic(R)^2 == .(format(ss$r.squared, digits = 2)))
RSME_label = bquote(italic(RSME) == .(format(sqrt(mean(ss$residuals^2)), digits = 2)))
n_label = bquote(italic(n) == .(format(nrow(df)), digits = 0))

## Plot
par(pty="s")
plot(df$x, df$y, xlab = "X", ylab = "Y")
abline(lm(df$y~df$x))
text(1, -7, R_label)
text(1, -10, RSME_label)
text(1, -13, n_label)

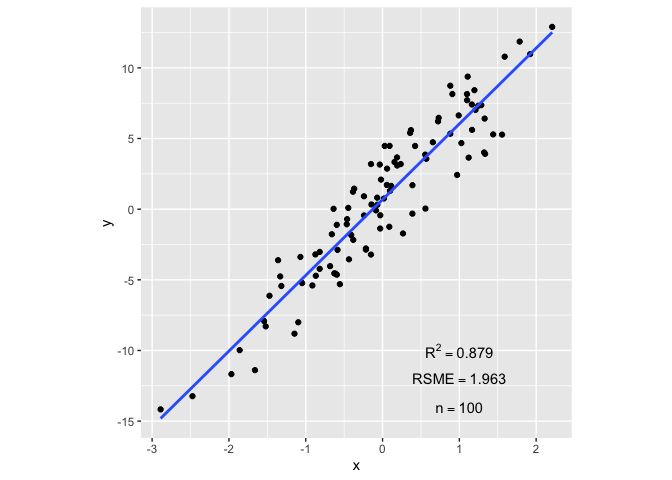
GGPLOT

library(ggplot2)
## create labels
my_label <- c(paste0("R^2 ==", round(ss$r.squared, 3)),
              paste("RSME ==", round(sqrt(mean(ss$residuals^2)), 3)),
              paste("n == ", nrow(df)))

## Plot
ggplot(df, aes(x=x, y=y))  
  geom_point()  
  geom_smooth(method = 'lm', se = F)  
  annotate(
    "text",
    x = 1, y = c(-10,-12, -14),
    label = my_label, parse = TRUE
  )  
  theme(aspect.ratio = 1)
#> `geom_smooth()` using formula = 'y ~ x'

DATA

set.seed(20)             
## Simulate predictor variable
x <- rnorm(100)          
## Simulate the error term
e <- rnorm(100, 0, 2)    
## Compute the outcome via the model
y <- 0.5   5 * x   e   
## make DF
df <- data.frame(x,y)