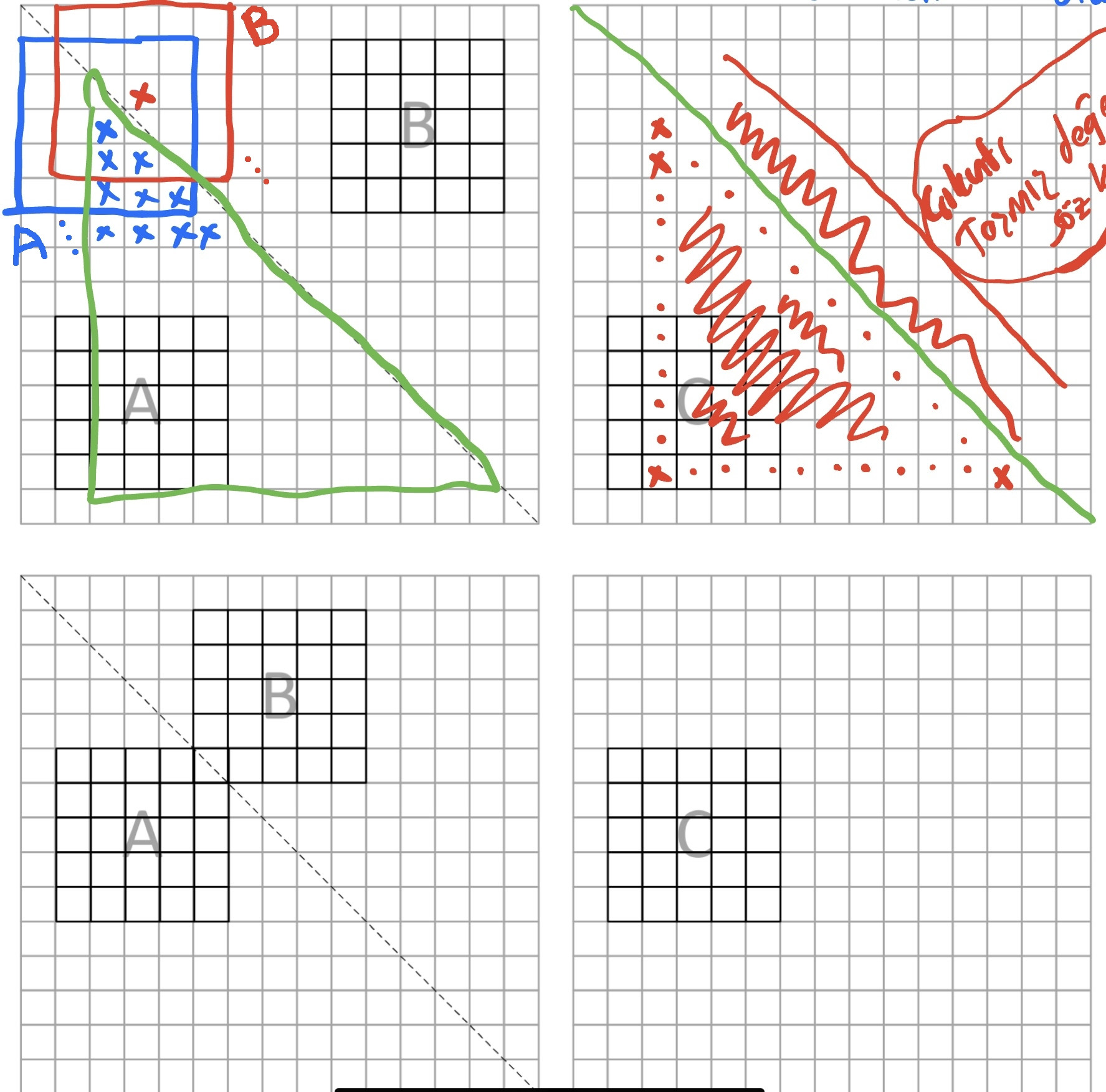
I have a matrix multiplication problem. We have an image matrix which can be have variable size. It is required to calculate C = A*B for every possible 5x5. C will be added to output image as seen in figure. The center point of A Matrix is located in the lower triangle. Also, B is placed diagonally symmetric to A. A can be overlap, so, B can be overlap too. Figures can be seen in below for more detailed understand:
Blue X points represent all possible mid points of A. Algorithm should just do multiply A and diagonally mirrored version of A or called B. I done it with lots of for loop. I need to reduce number of for that I used. Could you help me please?
What kind of algorithm can be used for this problem? I have some confusing points.
Could you please help me with your genius algorithm talents? Or could you direct me to an expert?
Original Questions is below:
Thanks.
Update:
#define SIZE_ARRAY 20
#define SIZE_WINDOW 5
#define WINDOW_OFFSET 2
#define INDEX_OFFSET 1
#define START_OFFSET_COLUMN 2
#define START_OFFSET_ROW 3
#define END_OFFSET_COLUMN 3
#define END_OFFSET_ROW 2
#define GET_LOWER_DIAGONAL_INDEX_MIN_ROW (START_OFFSET_ROW);
#define GET_LOWER_DIAGONAL_INDEX_MAX_ROW (SIZE_ARRAY - INDEX_OFFSET - END_OFFSET_ROW)
#define GET_LOWER_DIAGONAL_INDEX_MIN_COL (START_OFFSET_COLUMN);
#define GET_LOWER_DIAGONAL_INDEX_MAX_COL (SIZE_ARRAY - INDEX_OFFSET - END_OFFSET_COLUMN)
uint32_t lowerDiagonalIndexMinRow = GET_LOWER_DIAGONAL_INDEX_MIN_ROW;
uint32_t lowerDiagonalIndexMaxRow = GET_LOWER_DIAGONAL_INDEX_MAX_ROW;
uint32_t lowerDiagonalIndexMinCol = GET_LOWER_DIAGONAL_INDEX_MIN_COL;
uint32_t lowerDiagonalIndexMaxCol = GET_LOWER_DIAGONAL_INDEX_MAX_COL;
void parallelMultiplication_Stable_Master()
{
startTimeStamp = omp_get_wtime();
#pragma omp parallel for num_threads(8) private(outerIterRow, outerIterCol,rA,cA,rB,cB) shared(inputImage, outputImage)
for(outerIterRow = lowerDiagonalIndexMinRow; outerIterRow < lowerDiagonalIndexMaxRow; outerIterRow )
{
for(outerIterCol = lowerDiagonalIndexMinCol; outerIterCol < lowerDiagonalIndexMaxCol; outerIterCol )
{
if(outerIterCol 1 < outerIterRow)
{
rA = outerIterRow - WINDOW_OFFSET;
cA = outerIterCol - WINDOW_OFFSET;
rB = outerIterCol - WINDOW_OFFSET;
cB = outerIterRow - WINDOW_OFFSET;
for(i= outerIterRow - WINDOW_OFFSET; i <= outerIterRow WINDOW_OFFSET; i )
{
for(j= outerIterCol - WINDOW_OFFSET; j <= outerIterCol WINDOW_OFFSET; j )
{
for(k=0; k < SIZE_WINDOW; k )
{
#pragma omp critical
outputImage[i][j] = inputImage[rA][cA k] * inputImage[rB k][cB];
}
cB ;
rA ;
}
rB ;
cA ;
printf("Thread Number - %d",omp_get_thread_num());
}
}
}
}
stopTimeStamp = omp_get_wtime();
printArray(outputImage,"Output Image");
printConsoleNotification(100, startTimeStamp, stopTimeStamp);
}
I am getting segmentation fault error if I set up thread count more than "1". What is the trick ?
CodePudding user response:
Here is my take. I wrote this before OP showed any code, so I'm not following any of their code patterns.
I start with a suitable image struct, just for my own sanity.
struct Image
{
float* values;
int rows, cols;
};
struct Image image_allocate(int rows, int cols)
{
struct Image rtrn;
rtrn.rows = rows;
rtrn.cols = cols;
rtrn.values = malloc(sizeof(float) * rows * cols);
return rtrn;
}
void image_fill(struct Image* img)
{
ptrdiff_t row, col;
for(row = 0; row < img->rows; row)
for(col = 0; col < img->cols; col)
img->values[row * img->cols col] = rand() * (1.f / RAND_MAX);
}
void image_print(const struct Image* img)
{
ptrdiff_t row, col;
for(row = 0; row < img->rows; row) {
for(col = 0; col < img->cols; col)
printf("%.3f ", img->values[row * img->cols col]);
putchar('\n');
}
putchar('\n');
}
A 5x5 matrix multiplication is too small to reasonably dispatch to BLAS. So I write a simple version myself that can be loop-unrolled and / or inlined. This routine could use a couple of micro-optimizations but let's keep it simple for now.
/** out = left * right for 5x5 sub-matrices */
static void mat_mul_5x5(
float* restrict out, const float* left, const float* right, int cols)
{
ptrdiff_t row, col, inner;
float sum;
for(row = 0; row < 5; row) {
for(col = 0; col < 5; col) {
sum = out[row * cols col];
for(inner = 0; inner < 5; inner)
sum = left[row * cols inner] * right[inner * cols row];
out[row * cols col] = sum;
}
}
}
Now for the single-threaded implementation of the main algorithm. Again, nothing fancy. We just iterate over the lower triangular matrix, excluding the diagonal. I keep track of the top-left corner instead of the center point. Makes index computation a bit simpler.
void compute_ltr(struct Image* restrict out, const struct Image* in)
{
ptrdiff_t top, left, end;
/* if image is not quadratic, find quadratic subset */
end = out->rows < out->cols ? out->rows : out->cols;
assert(in->rows == out->rows && in->cols == out->cols);
memset(out->values, 0, sizeof(float) * out->rows * out->cols);
for(top = 1; top <= end - 5; top)
for(left = 0; left < top; left)
mat_mul_5x5(out->values top * out->cols left,
in->values top * in->cols left,
in->values left * in->cols top,
in->cols);
}
The parallelization is a bit tricky because we have to make sure the threads don't overlap in their output matrices. A critical section, atomics or similar stuff would cost too much performance.
A simpler solution is a strided approach: If we always keep the threads 5 rows apart, they cannot interfere. So we simply compute every fifth row, synchronize all threads, then compute the next set of rows, five apart, and so on.
void compute_ltr_parallel(struct Image* restrict out, const struct Image* in)
{
/* if image is not quadratic, find quadratic subset */
const ptrdiff_t end = out->rows < out->cols ? out->rows : out->cols;
assert(in->rows == out->rows && in->cols == out->cols);
memset(out->values, 0, sizeof(float) * out->rows * out->cols);
/*
* Keep the parallel section open for multiple loops to reduce
* overhead
*/
# pragma omp parallel
{
ptrdiff_t top, left, offset;
for(offset = 0; offset < 5; offset) {
/* Use dynamic scheduling because the work per row varies */
# pragma omp for schedule(dynamic)
for(top = 1 offset; top <= end - 5; top = 5)
for(left = 0; left < top; left)
mat_mul_5x5(out->values top * out->cols left,
in->values top * in->cols left,
in->values left * in->cols top,
in->cols);
}
}
}
My benchmark with 1000 iterations of a 1000x1000 image show 7 seconds for the serial version and 1.2 seconds for the parallelized version on my 8 core / 16 thread CPU.
CodePudding user response:
I'm not providing a solution, but some thoughts that may help the OP exploring a possible approach.
You can evaluate each element of the resulting C matrix directly, from the values of the original matrix in a way similar to a 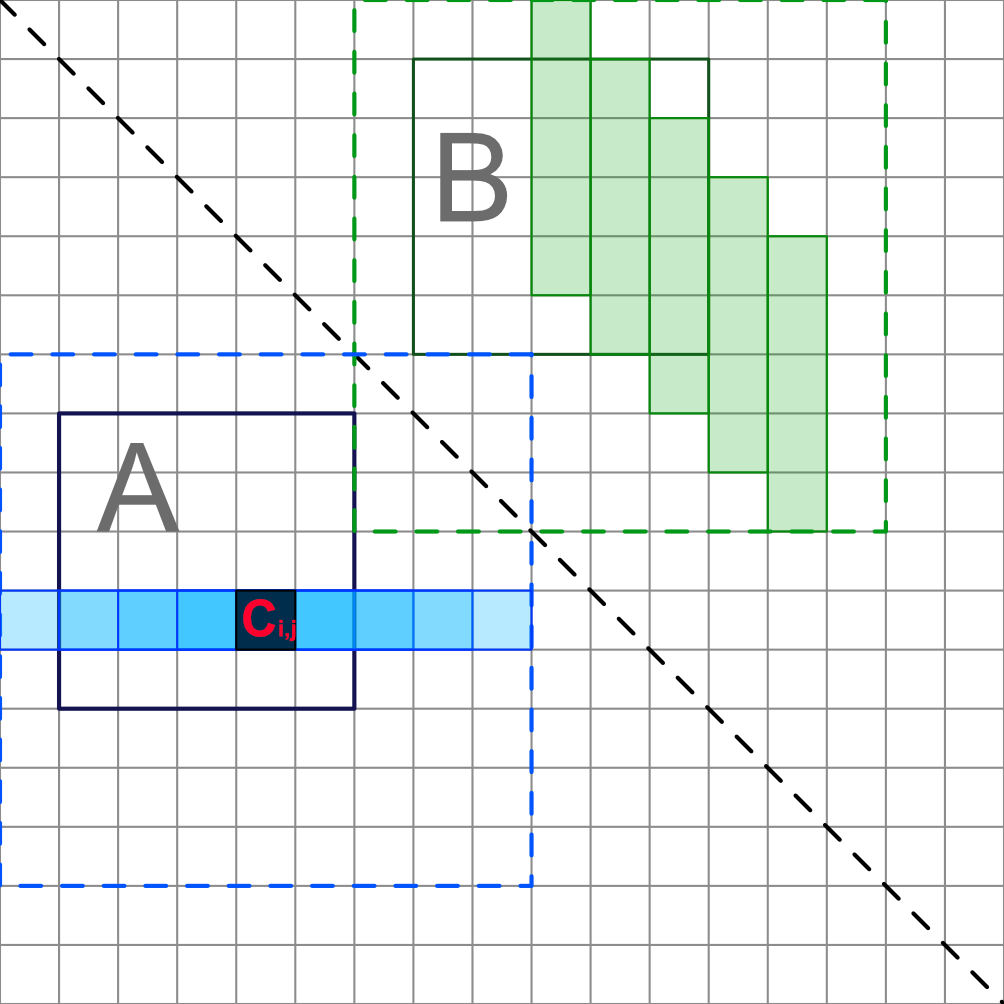
Instead of computing each matrix product for every A submatrix, you can evaluate the value of each Ci, j from the values in the shaded areas.
Note that Ci, j depends only on a small subset of row i and that the elements of the upper right triangular submatrix (where the B submatrices are picked) could be copied and maybe transposed in a more chache-friendly accomodation.
Alternatively, it may be worth exploring an approach where for every possible Bi, j, all the corresponding elements of C are evaluated.