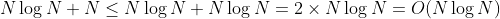I understand that if time complexity of an algorithm is c * O(N), where c is a constant, we can ignore c and complexity is same as O(N).

Can we do same if its O(N) c.

I have this doubt because for an algorithm which involves sorting and scanning(like finding unique elements in an array), various texts state its complexity to be N *log(N).

If we take both steps, then its:

Sorting: N*log(N) Scanning: N

So total time is N * (log(N) 1).

CodePudding user response：

Recall that

In fact, we can make the rule more general. E.g.,

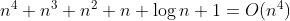
For a polynomial, Big O is determined by the term with highest/fastest order, and we may disregard lower-order terms of the polynomial. Wikipedia has some explanation.

CodePudding user response：

O(f(n)) = lim(x->inf) f(x n)/f(x)