Projecting 2D Generated Mesh onto 3D Uniform grid-CodePudding

I have the following patterned mesh in 2D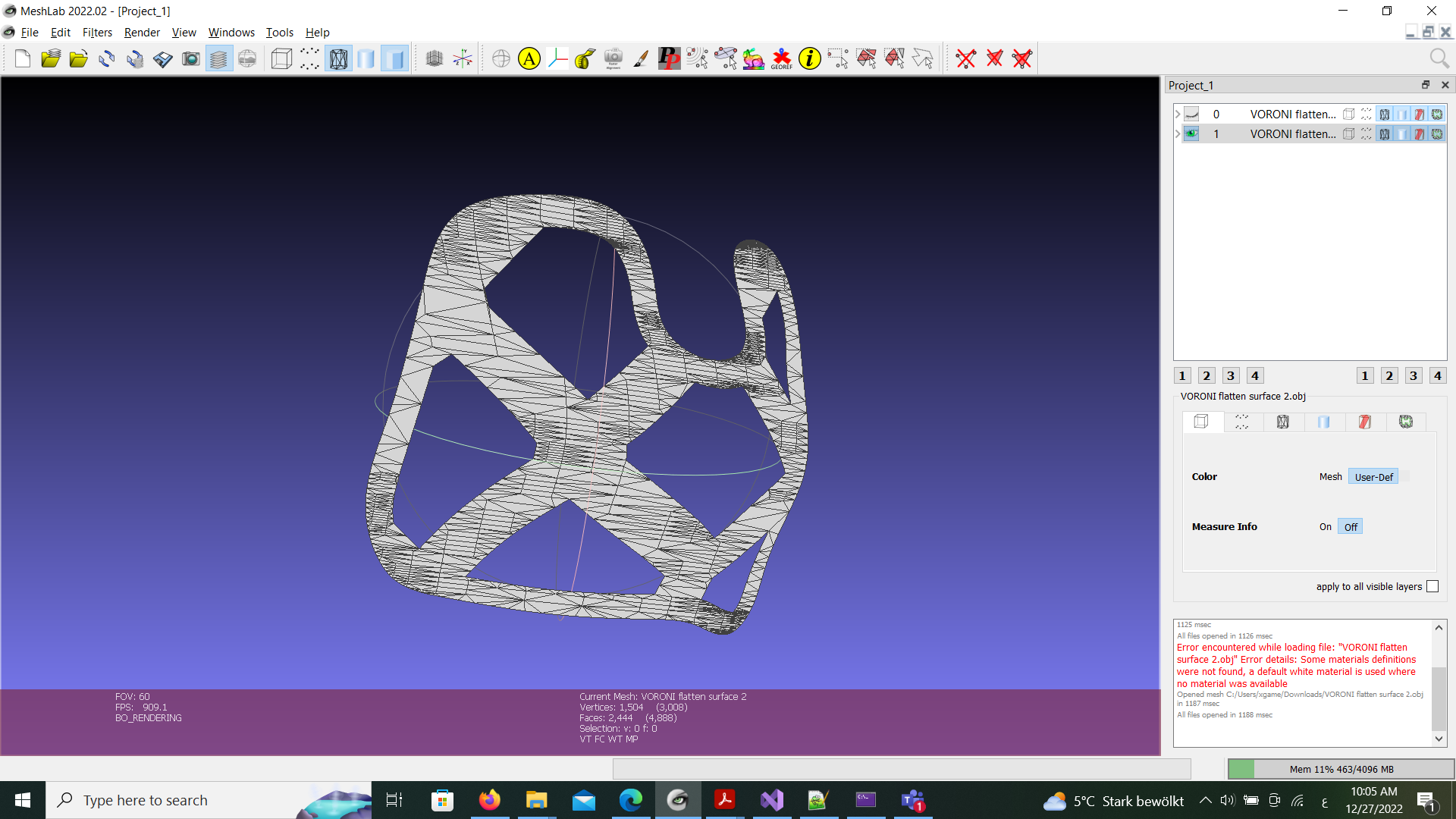

I have a curved grid of 3D Uniform points

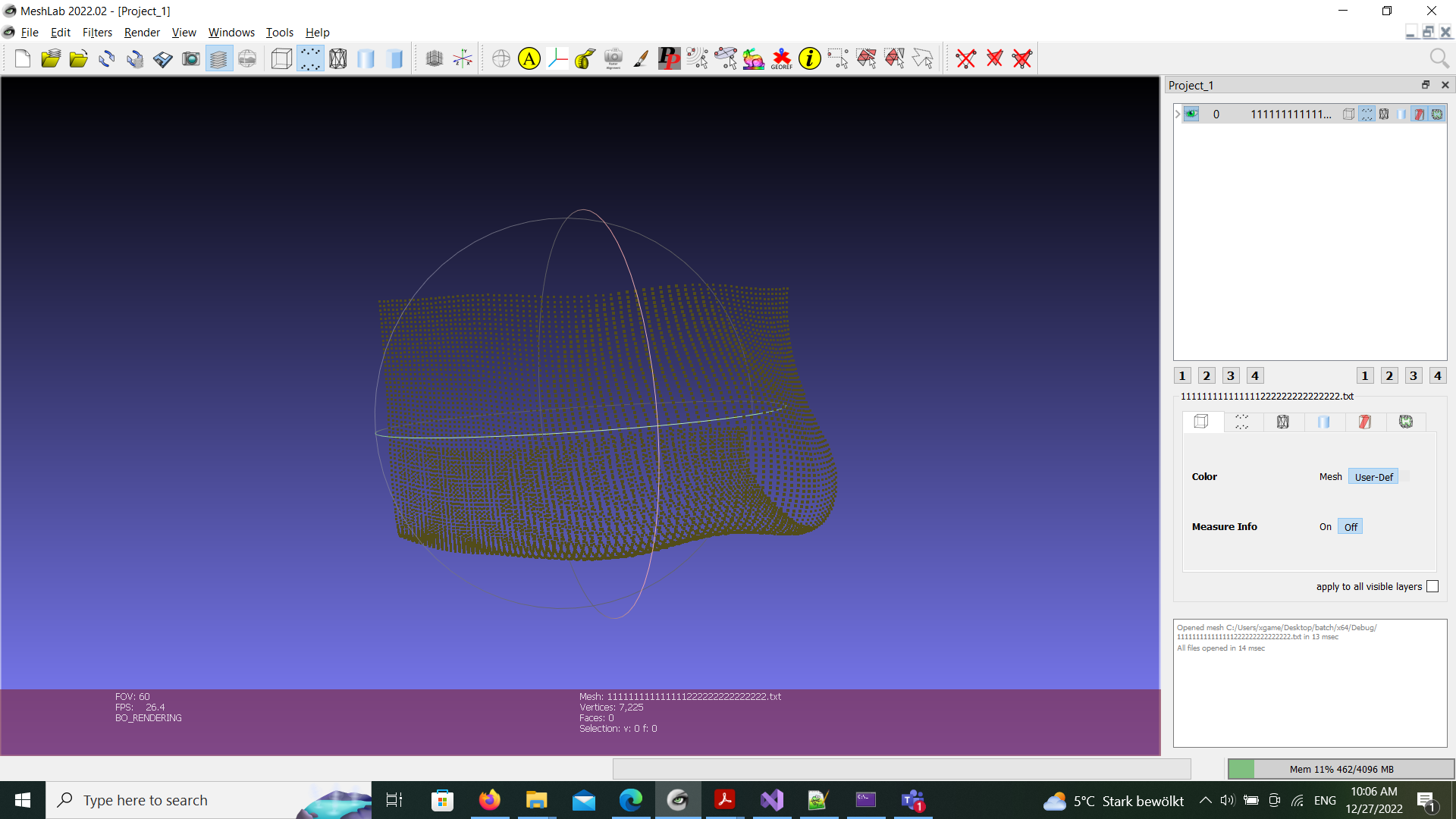
My trial:

The patterned mesh is from UV coordinates 0 to 1 mapped to those values
using cubic interpolation, I'm getting a point on the Curved Mesh
Using the indices of the patterned mesh I get a result mesh with the points that are interpolated from #2

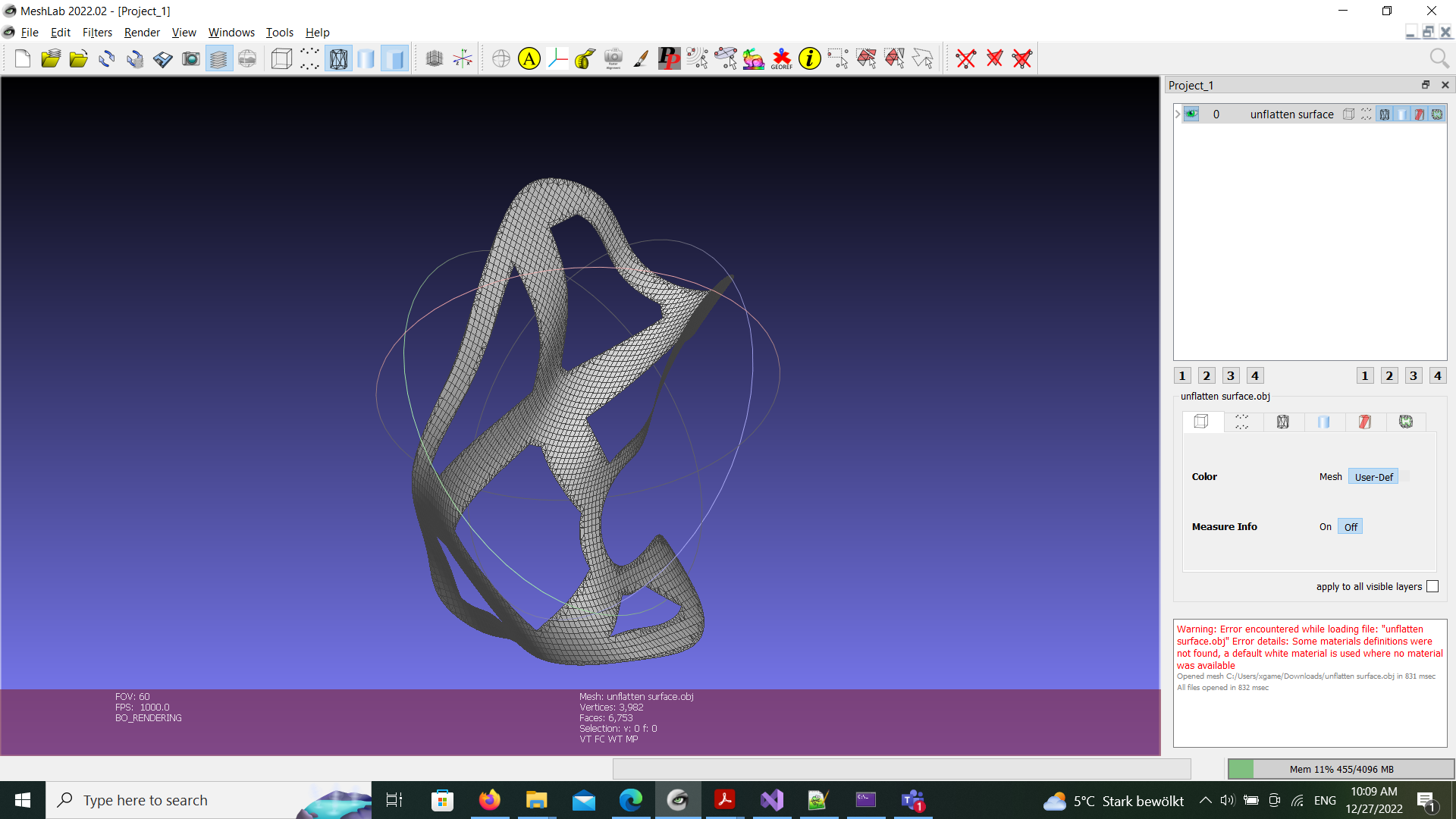
The problem is I get a flattened curved mesh as shown it doesn't have the required depth due to using 2D Coordinates in the patterned mesh:

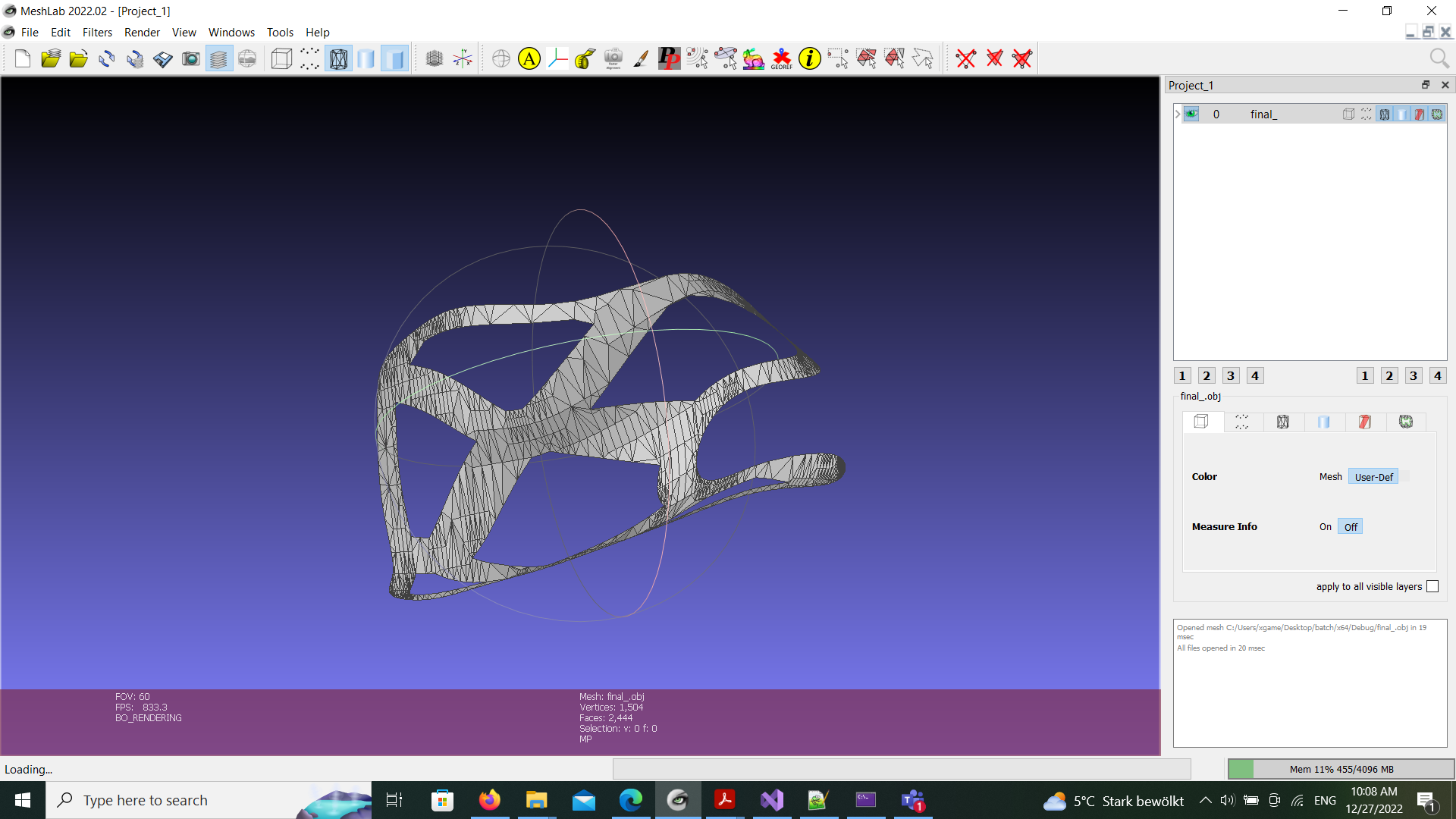
While the result mesh should look like this:

I'm using the following code to do the purpose:

std::vector<glm::vec3> voronoi_project_to_3D(std::vector<glm::vec3> &voronoi_pnts)
{
    int i, iu, iv;
    float u, v;
    vec2 p0{}, p1{};
    vec3 p;
    vec3 c[4 * 4];
    std::vector < glm::vec3> points_3d;
    // compute BBOX of 2D voronoi
    for (i = 0; i < voronoi_pnts.size(); i  )
    {
        p = voronoi_pnts[i];
        if (!i) { p0 = p; p1 = p; }
        if (p0.x > p.x) p0.x = p.x;
        if (p1.x < p.x) p1.x = p.x;
        if (p0.y > p.y) p0.y = p.y;
        if (p1.y < p.y) p1.y = p.y;
    }
    // convert ot 3D
    p1.x = float(mesh_nu-35) / (p1.x - p0.x);
    p1.y = float(mesh_nv-35) / (p1.y - p0.y);
    for (i = 0; i < voronoi_pnts.size(); i  )
    {
        p = voronoi_pnts[i];
        u = (p.x - p0.x) * p1.x;
        v = (p.y - p0.y) * p1.y;
        iu = floor(u); u -= iu;
        iv = floor(v); v -= iv;
        cubic_surface_set_it4(c,
            mesh_pnt   iu   ((iv   0) * mesh_nu),
            mesh_pnt   iu   ((iv   1) * mesh_nu),
            mesh_pnt   iu   ((iv   2) * mesh_nu),
            mesh_pnt   iu   ((iv   3) * mesh_nu));
        points_3d.push_back(cubic_surface_get_it4(c, u, v));
    }
    return points_3d;
}

CodePudding user response：

the problem is in the scaling from BBOX to u,v and iu,iv ... as the target is piecewise cubic surface patch of resolution mesh_nu,mesh_nv control points we need to select 4x4 control points starting with index 0,0 and ending with mesh_nu-3,mesh_nv-3 as cubic surface need 4 points per patch and axis so the code should be:

std::vector<glm::vec3> voronoi_project_to_3D(std::vector<glm::vec3> &voronoi_pnts)
{
    int i, iu, iv;
    float u, v;
    vec2 p0{}, p1{};
    vec3 p;
    vec3 c[4 * 4];
    std::vector < glm::vec3> points_3d;
    // compute BBOX of 2D voronoi
    for (i = 0; i < voronoi_pnts.size(); i  )
    {
        p = voronoi_pnts[i];
        if (!i) { p0 = p; p1 = p; }
        if (p0.x > p.x) p0.x = p.x;
        if (p1.x < p.x) p1.x = p.x;
        if (p0.y > p.y) p0.y = p.y;
        if (p1.y < p.y) p1.y = p.y;
    }
    // convert ot 3D
    p1.x = float(mesh_nu-3) / (p1.x - p0.x);
    p1.y = float(mesh_nv-3) / (p1.y - p0.y);
    for (i = 0; i < voronoi_pnts.size(); i  )
    {
        p = voronoi_pnts[i];
        u = (p.x - p0.x) * p1.x;
        v = (p.y - p0.y) * p1.y;
        iu = floor(u); u -= iu;
        iv = floor(v); v -= iv;
        cubic_surface_set_it4(c,
            mesh_pnt   iu   ((iv   0) * mesh_nu),
            mesh_pnt   iu   ((iv   1) * mesh_nu),
            mesh_pnt   iu   ((iv   2) * mesh_nu),
            mesh_pnt   iu   ((iv   3) * mesh_nu));
        points_3d.push_back(cubic_surface_get_it4(c, u, v));
    }
    return points_3d;
}

Note I changed the -35 to -3 in order to work properly the constants mesh_nu,mesh_nv must match the cubic surface control points mesh_pnt topology...

For those of you that do not have context to this QA here full VCL/OpenGL source (BDS2006 C Builder) and win32 binary:

Win32 OpenGL/VCL C example for cubic surface and 2D mesh projection onto it

The example also contains my GLSL_math.h template and newest version of gl_simple.h (supporting geometry shaders) which I often use for SO code examples in my answers... Here also related chat (containing all the info about the stuff behind it):

chat