Numpy.linalg.norm performance apparently doesn't scale with the number of dimensions-CodePudding

I have the following snippets of code which is a subroutine of the K-means clustering algorithm; specifically, it tries to assign each point to the closest centroid.

import numpy as np

n = 20000
D = 30
K = 250

points = np.random.rand(n, D)
centroids = np.random.rand(K, D)
membership = np.zeros(shape=n, dtype=int)
for i in range(n):
    distances = np.apply_along_axis(lambda x: np.linalg.norm(x, ord=2), 1, centroids - points[i])
    membership[i] = np.argmin(distances)

The running time here should be O(NKD) where D is the dimension of the data points, so naturally I expect when D increases or decreases, the running time would change proportionally as well. To my surprise, I see very little time being changed when changing D, for example when testing on my local machine:

D = 1
python3 benchmark.py  12.10s user 0.39s system 118% cpu 10.564 total

D = 30
python3 benchmark.py  12.17s user 0.36s system 117% cpu 10.703 total

D = 300
python3 benchmark.py  13.30s user 0.31s system 115% cpu 11.784 total

D = 1000
python3 benchmark.py  16.51s user 1.76s system 110% cpu 16.524 total

Is there something that I'm missing here?

CodePudding user response：

This is due to the overhead of Numpy functions.

Indeed, np.apply_along_axis is called 20_000 times and each call to this function internally does a loop calling the target Python function 250 times (ie. it is not vectorized), and so np.linalg.norm. In the end, np.linalg.norm is called, 20_000 * 250 = 5000000 times. The thing is each call to a Numpy function takes typically about 1 µs. On my machine, np.linalg.norm takes 4-5 µs on an array of size 1. This time is due to many internal checks (types and values), allocations, functions calls, conversion, etc.

There are two simple ways to reduce this overhead: vectorization and using a JIT compiler like Numba. The later is often more efficient as it avoid creating expensive big temporary arrays.

Here is a much faster implementation:

import numpy as np
import numba as nb

@nb.njit('(float64[:,::1], float64[:,::1], int_[::1])')
def compute(points, centroids, membership):
    n, K, D = points.shape[0], centroids.shape[0], points.shape[1]
    assert centroids.shape[1] == D and membership.shape[0] == n
    distances = np.empty(K, np.float64)
    for i in range(n):
        for j in range(K):
            distances[j] = np.linalg.norm(centroids[j] - points[i], ord=2)
        membership[i] = np.argmin(distances)

n = 20000
D = 30
K = 250

points = np.random.rand(n, D)
centroids = np.random.rand(K, D)
membership = np.zeros(shape=n, dtype=int)

compute(points, centroids, membership)

In fact, while this code is much faster, it still have a similar issue: the cost of allocating the temporary arrays centroids[j] - points[i] is significant compared to the actual time required to compute the norm. In fact, each allocations takes only few hundred of nanoseconds, but the number of loop iteration is huge. One solution is simply to compute the norm manually:

from math import sqrt

@nb.njit('(float64[:,::1], float64[:,::1], int_[::1])', fastmath=True)
def compute_fast(points, centroids, membership):
    n, K, D = points.shape[0], centroids.shape[0], points.shape[1]
    assert centroids.shape[1] == D and membership.shape[0] == n
    distances = np.empty(K, np.float64)
    for i in range(n):
        for j in range(K):
            s = 0.0
            for k in range(D):
                tmp = centroids[j,k] - points[i,k]
                s  = tmp * tmp
            distances[j] = sqrt(s)
        membership[i] = np.argmin(distances)

Here are results on my i5-9600KF processor:

D=1:
    initial code:   26.56 seconds
    compute:         1.44 seconds
    compute_fast:    0.02 seconds  (x1328)
D=30:
    initial code:   27.09 seconds
    compute:         1.65 seconds
    compute_fast:    0.13 seconds  (x208)
D=1000:
    initial code:   39.34 seconds
    compute:         3.74 seconds
    compute_fast:    4.57 seconds  (x8.6)

The last implementation is much faster for small values of D since the Numpy overhead are the main bottleneck in this case and the implementation can almost completely remove such overheads (thanks to the JIT compilation).

CodePudding user response：

It is probably O(NKD).

But the thing is you are iterating 3 loops here. One explicitly. One semi-explicitly. And the last one implicitly, inside numpy functions.

The outer one is your explicit for loop, for N.

The middle one is the np.apply_along_axis one, which applies on the K rows of centroids-points[i] (btw, there is another one here, with some broadcasting. But we don't need to count all of them for big-O consideration)

And the inner one is the one on the D columns that occur inside norm.

The inner one is obviously the most important to optimized, and that's good, because it is the only one that is vectorized here.

But that means that for small enough value of D, what we really see is more some constant overhead (times N×K, since it is inside a double for loop). Your inefficient outer for loops drive most of the cost, which, then, looks like O(NK).

Note that np.apply_along_axis is just a for loop by another name. It is not as bad. But almost so. It is still calling several times some python code. It is not vectorization.

But, well, I bet that with D big enough, you'll see that it is O(NKD)

Edit:

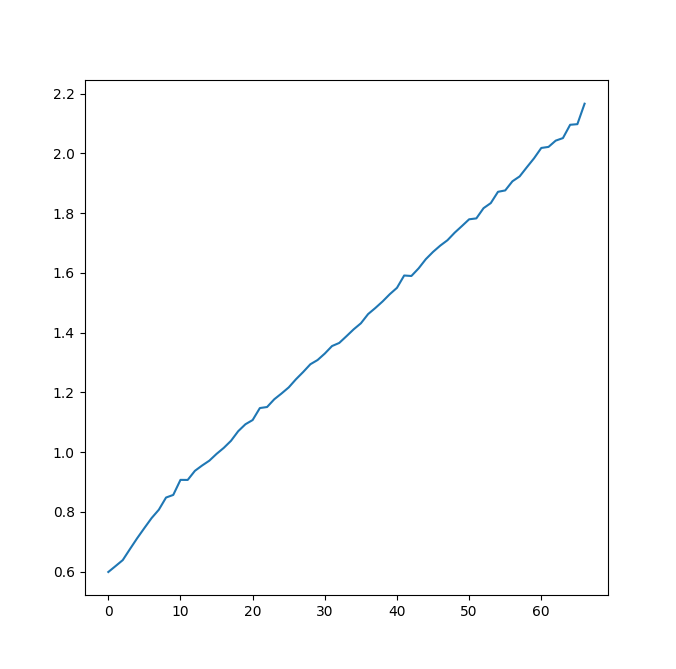
Here is what I get when I increase D (with smaller n, so that it remains computable in realistic time)

You see that it looks really linear (affine, to be accurate, since it doesn't pass through 0, which is the reason why it doesn't look very linear to you; and which is explained by my previous comment: most of the inner cost inside the for/along_axis double loop is mainly constant overhead of those loops, when D is small. The "proportional to D" part begins to show when the overhead become negligible)