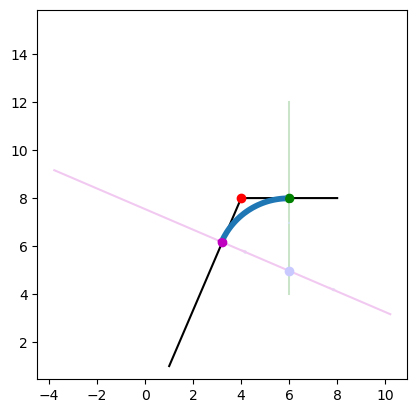
I'm trying to draw an arc of n number of steps between two points so that I can bevel a 2D shape. This image illustrates what I'm looking to create (the blue arc) and how I'm trying to go about it:

1. move by the radius away from the target point (red)
2. get the normals of those lines
3. get the intersections of the normals to find the center of the circle
4. Draw an arc between those points from the circle's center

This is what I have so far:

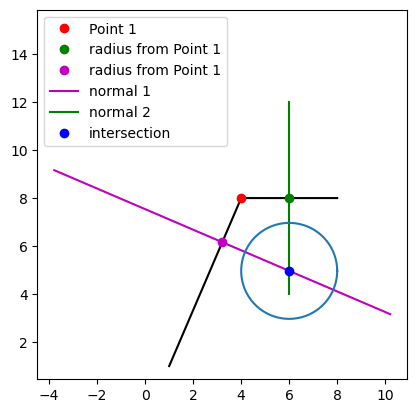
As you can see, the circle is not tangent to the line segments. I think my approach may be flawed thinking that the two points used for the normal lines should be moved by the circle's radius. Can anyone please tell me where I am going wrong and how I might be able to find this arc of points? Here is my code:

import matplotlib.pyplot as plt
import numpy as np

#https://stackoverflow.com/questions/51223685/create-circle-tangent-to-two-lines-with-radius-r-geometry

def travel(dx, x1, y1, x2, y2):
    a = {"x": x2 - x1, "y": y2 - y1}
    mag = np.sqrt(a["x"]*a["x"]   a["y"]*a["y"])
    
    if (mag == 0):
        a["x"] = a["y"] = 0;
    else:
        a["x"] = a["x"]/mag*dx
        a["y"] = a["y"]/mag*dx

    return [x1   a["x"], y1   a["y"]]

def plot_line(line,color="go-",label=""):
    plt.plot([p[0] for p in line],
             [p[1] for p in line],color,label=label)

def line_intersection(line1, line2):
    xdiff = (line1[0][0] - line1[1][0], line2[0][0] - line2[1][0])
    ydiff = (line1[0][1] - line1[1][1], line2[0][1] - line2[1][1])

    def det(a, b):
        return a[0] * b[1] - a[1] * b[0]

    div = det(xdiff, ydiff)
    if div == 0:
       raise Exception('lines do not intersect')

    d = (det(*line1), det(*line2))
    x = det(d, xdiff) / div
    y = det(d, ydiff) / div
    return x, y
    
line_segment1 = [[1,1],[4,8]]
line_segment2 = [[4,8],[8,8]]
line = line_segment1   line_segment2
plot_line(line,'k-')
radius = 2

l1_x1 = line_segment1[0][0]
l1_y1 = line_segment1[0][1]
l1_x2 = line_segment1[1][0]
l1_y2 = line_segment1[1][1]
new_point1 = travel(radius, l1_x2, l1_y2, l1_x1, l1_y1)

l2_x1 = line_segment2[0][0]
l2_y1 = line_segment2[0][1]
l2_x2 = line_segment2[1][0]
l2_y2 = line_segment2[1][1]
new_point2 = travel(radius, l2_x1, l2_y1, l2_x2, l2_y2)

plt.plot(line_segment1[1][0], line_segment1[1][1],'ro',label="Point 1")
plt.plot(new_point2[0], new_point2[1],'go',label="radius from Point 1")
plt.plot(new_point1[0], new_point1[1],'mo',label="radius from Point 1")

# normal 1
dx = l1_x2 - l1_x1
dy = l1_y2 - l1_y1
normal_line1 = [[new_point1[0] -dy, new_point1[1] dx],[new_point1[0] dy, new_point1[1] -dx]]
plot_line(normal_line1,'m',label="normal 1")

# normal 2
dx2 = l2_x2 - l2_x1
dy2 = l2_y2 - l2_y1
normal_line2 = [[new_point2[0] -dy2, new_point2[1] dx2],[new_point2[0] dy2, new_point2[1] -dx2]]
plot_line(normal_line2,'g',label="normal 2")

x, y = line_intersection(normal_line1,normal_line2)
plt.plot(x, y,'bo',label="intersection") #'blue'

theta = np.linspace( 0 , 2 * np.pi , 150 )
a = x   radius * np.cos( theta )
b = y   radius * np.sin( theta )
plt.plot(a, b)
plt.legend()
plt.axis('square')
plt.show()

Thanks a lot!

CodePudding user response：

You could try making a Bezier curve, like in this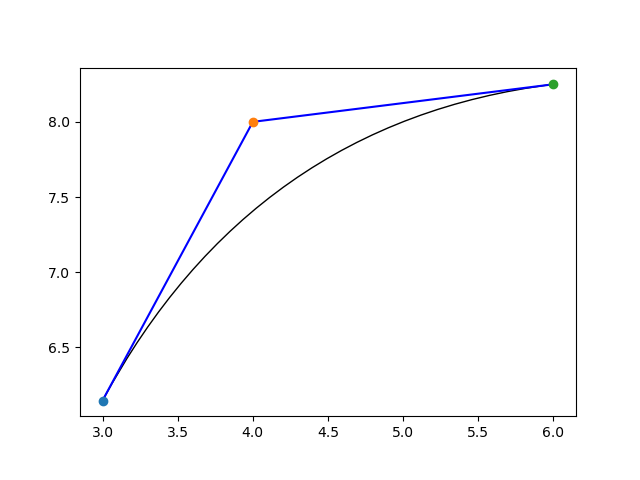

To do this without using a Matplotlib PathPatch object, you can calculate the Bezier points as, for example, in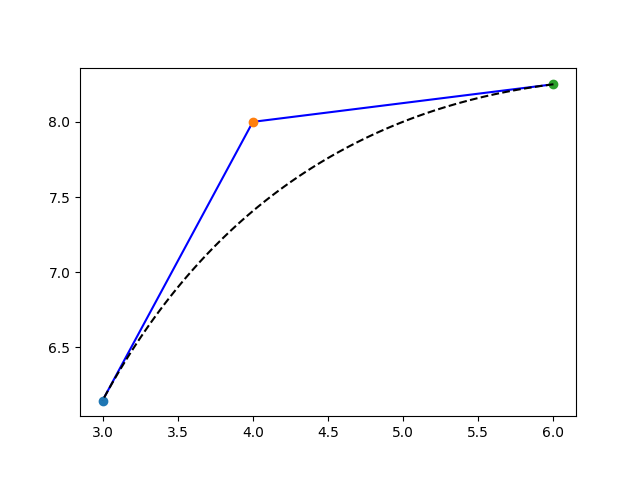

CodePudding user response：

If you are not just interested in the solution but in better understanding of this problem, you should read the article on Curved Paths that Amit Patel wrote in his 'Red Blob Games' blog.

https://www.redblobgames.com/articles/curved-paths/