How to get connected components label in a binary image?-CodePudding

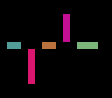
I've a binary image where removing green dot gets me separate line segments. I've tried using label_components() function from Julia but it labels only verticall joined pixels as one label. I'm using

using Images
img=load("current_img.jpg")
img[findall(img.==RGB(0.0,0.1,0.0))].=0 # this makes green pixels same as background, i.e. black
labels = label_components(img)

I'm expecteing all lines which are disjoint to be given a unique label (as was a funciton in connected component labeling in matlab, but i can't find something similar in julia)

CodePudding user response：

Since you updated the question and added more details to make it clear, I decided to post the answer. Note that this answer utilizes some of the functions that I wrote

I want to perform a segmentation process on it and labelize each segment and highlight the segments using the achieved labels.
Let's define the functions:

using Images
using ImageBinarization

function check_adjacent(
  loc::CartesianIndex{2},
  all_locs::Vector{CartesianIndex{2}}
  )

  conditions = [
    loc - CartesianIndex(0,1) ∈ all_locs,
    loc   CartesianIndex(0,1) ∈ all_locs,
    loc - CartesianIndex(1,0) ∈ all_locs,
    loc   CartesianIndex(1,0) ∈ all_locs,
    loc - CartesianIndex(1,1) ∈ all_locs,
    loc   CartesianIndex(1,1) ∈ all_locs,
    loc - CartesianIndex(1,-1) ∈ all_locs,
    loc   CartesianIndex(1,-1) ∈ all_locs
  ]

  return sum(conditions)
end;

function find_the_contour_branches(img::BitMatrix)
  img_matrix = convert(Array{Float64}, img)
  not_black = findall(!=(0.0), img_matrix)
  contours_branches = Vector{CartesianIndex{2}}()
  for nb∈not_black
    t = check_adjacent(nb, not_black)
    (t==1 || t==3) && push!(contours_branches, nb)
  end
  return contours_branches
end;

"""
  HighlightSegments(img::BitMatrix, labels::Matrix{Int64})

Highlight the segments of the image with random colors.

# Arguments
- `img::BitMatrix`: The image to be highlighted.
- `labels::Matrix{Int64}`: The labels of each segment.

# Returns
- `img_matrix::Matrix{RGB}`: A matrix of RGB values.
"""
function HighlightSegments(img::BitMatrix, labels::Matrix{Int64})
  colors = [
    # Create Random Colors for each label
    RGB(rand(), rand(), rand()) for label in 1:maximum(labels)
  ]

  img_matrix = convert(Matrix{RGB}, img)

  for seg∈1:maximum(labels)
    img_matrix[labels .== seg] .= colors[seg]
  end

  return img_matrix
end;

"""
  find_labels(img_path::String)

Assign a label for each segment.

# Arguments
- `img_path::String`: The path of the image.

# Returns
- `thinned::BitMatrix`: BitMatrix of the thinned image.
- `labels::Matrix{Int64}`: A matrix that contains the labels of each segment.
- `highlighted::Matrix{RGB}`: A matrix of RGB values.
"""
function find_labels(img_path::String)
  img::Matrix{RGB} = load(img_path)
  gimg = Gray.(img)
  bin::BitMatrix = binarize(gimg, UnimodalRosin()) .> 0.5
  thinned = thinning(bin)
  contours = find_the_contour_branches(thinned)
  thinned[contours] .= 0
  labels = label_components(thinned, trues(3,3))
  highlighted = HighlightSegments(thinned, labels)

  return thinned, labels, highlighted
end;

The main function in the above is find_labels which returns

The thinned matrix.
The labels of each segment.
The highlighted image (Matrix, actually).

First, I load the image, and binarize the Gray scaled image. Then, I perform the thinning operation on the binarized image. After that, I find the contours and the branches using the find_the_contour_branches function. Then, I turn the color of contours and branches to black in the thinned image; this gives me neat segments. After that, I labelize the segments using the label_components function. Finally, I highlight the segments using the HighlightSegments function for the sake of visualization (this is the bonus :)).
Let's try it on the image I drew above:

result = find_labels("nU3LE.png")

# you can get the labels Matrix using `result[2]`
# and the highlighted image using `result[3]`
# Also, it's possible to save the highlighted image using:
save("nU3LE_highlighted.png", result[3])

The result is as follows:

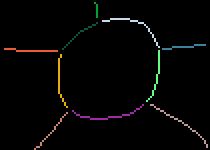
Also, I performed the same thing on another image:

julia> result = find_labels("circle.png")

julia> result[2]
14×16 Matrix{Int64}:
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  4  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  4  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  4  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  4  0  0  0  0  0  0
 0  1  1  0  0  0  3  3  0  0  0  5  5  5  0  0
 0  0  0  0  2  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  2  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  2  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  2  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  2  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0

As you can see, the labels are pretty clear. Now let's see the results of performing the procedure in some examples in one glance:

Original Image	Labeled Image