We have a problem (stated to be NP Hard) as follows:
Given a connected undirected unweighted graph G = (V, E) and a set of routes (a sequence of vertices) from homes to offices (there can be multiple routes starting from homes, and multiple routes ending at offices), we want to place minimum electric charging stations such that all routes are covered at least once. We cannot place stations at homes or offices.
The below image shows a possible input (please ignore the weights):
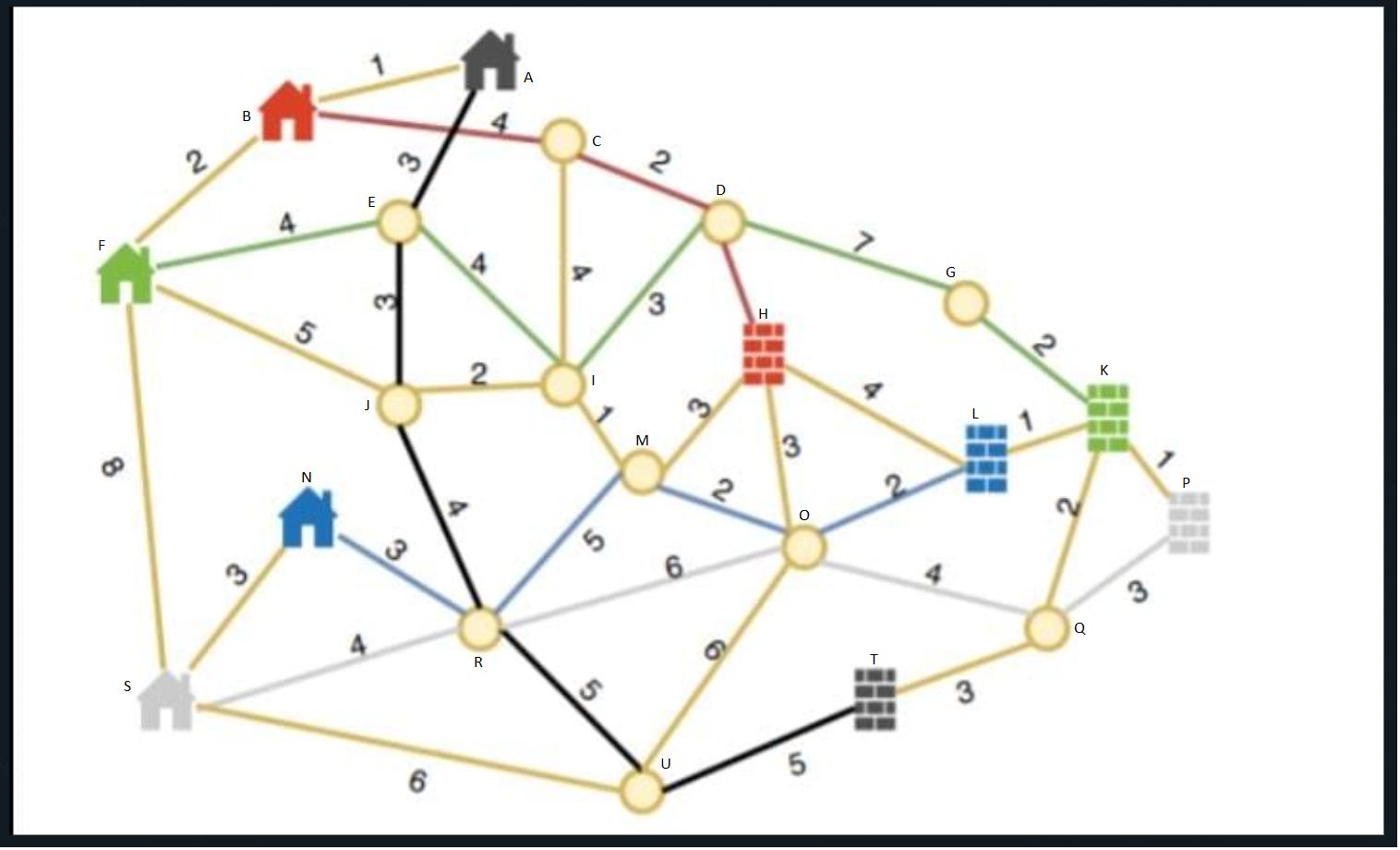
Where the house icons are homes and brick wall icons are offices.
The optimal above is placing stations at vertices R and D.
Finding the optimal solution is said to be an NP Hard problem.
I have an approach, which goes something like this:
Let S be empty set of charging stations (vertices)
Let R be set of all given routes, r_i = <v_0, v_1 ... v_j> where v_0 is of type "home" and v_j is of type "office"
Let Vdeg be array of integers of size |V| intially set to 0
For r in R:
Increment Vdeg of every vertex v in r
while R is not empty:
Sort vertices by decreasing Vdeg
Let maxDeg be maximum degree vertex in V
Add maxDeg to S
for all routes r in R which contains maxDeg
R = R\{r}
Decrement Vdeg for maxDeg
The above algorithm runs in (I believe) polynomial time, and also (I believe) gives the optimal solution.
The full implementation is given below:
#include <iostream>
#include <vector>
// A Graph Vertice
struct node {
int id;
std::string type;
std::string name;
};
std::ostream& operator <<(std::ostream& out, const node& n) {
return out << "{ " << n.type << ", " << n.name << " }";
}
// A Graph Edge
struct edge {
node * from;
node * to;
int weight;
};
std::ostream& operator <<(std::ostream& out, const edge& e) {
return out << "{ " << *e.from << ", " << *e.to << ", " << e.weight << " }";
}
std::ostream& operator <<(std::ostream& out, const std::vector<edge>& graph) {
out << "{ ";
for(int i = 0; i < graph.size(); i) {
out << graph[i] << ", ";
}
return out << "\b\b }";
}
std::ostream& operator <<(std::ostream& out, const std::vector<node*>& vertices) {
out << "{ ";
for(int i = 0; i < vertices.size(); i) {
out << "\n " << *vertices[i] << ", ";
}
return out << "\b\b \n}";
}
std::ostream& operator <<(std::ostream& out, const std::vector<edge*>& graph) {
out << "{ ";
for(int i = 0; i < graph.size(); i) {
out << "\n " << *graph[i] << ", ";
}
return out << "\b\b \n}";
}
std::ostream& operator <<(std::ostream& out, const std::vector<std::vector<edge*>>& graph) {
out << "{";
for(int i = 0; i < graph.size(); i) {
out << "\n " << graph[i] << ", ";
}
return out << "\b\b \n}";
}
// A Vdeg which also stores id and routes intersecting on it
struct vertice_degrees {
int id;
int degree;
std::vector<int> intersecting;
};
// Greater than operator overloaded for sorting Vdegs by degree
bool operator >(const vertice_degrees& vd1, const vertice_degrees& vd2) {
return vd1.degree > vd2.degree;
}
std::ostream& operator <<(std::ostream& out, const std::vector<vertice_degrees>& vd) {
out << "{ ";
for(int i = 0; i < vd.size(); i) {
out << "{ " << vd[i].id << ", " << vd[i].degree << ", { ";
for(int j = 0; j < vd[i].intersecting.size(); j) {
out << vd[i].intersecting[j] << ", ";
}
out << "\b\b }, ";
}
return out << "\b\b }";
}
void print_routes(const std::string label, const std::vector<int> routes_to_cover, const std::vector<std::vector<edge*>> routes, const std::string label_after) {
std::cout << label << "{ ";
for(int i = 0; i < routes_to_cover.size(); i) {
std::cout << routes[routes_to_cover[i]] << ", ";
}
std::cout << "\b\b }" << label_after;
}
int main() {
// List of vertices in graph
node vertices[] = {
node{ 0, "House", "A" },
node{ 1, "House", "B" },
node{ 2, "House", "F" },
node{ 3, "House", "N" },
node{ 4, "House", "S" },
node{ 5, "Office", "H" },
node{ 6, "Office", "K" },
node{ 7, "Office", "L" },
node{ 8, "Office", "P" },
node{ 9, "Office", "T" },
node{ 10, "None", "C" },
node{ 11, "None", "D" },
node{ 12, "None", "E" },
node{ 13, "None", "G" },
node{ 14, "None", "I" },
node{ 15, "None", "J" },
node{ 16, "None", "M" },
node{ 17, "None", "O" },
node{ 18, "None", "Q" },
node{ 19, "None", "R" },
node{ 20, "None", "U" }
};
// Length of vertices array
const int vertice_count = sizeof(vertices)/sizeof(node);
// List of edges in graph
std::vector<edge> graph = {
edge{ &vertices[0], &vertices[12], 3 },
edge{ &vertices[12], &vertices[15], 3 },
edge{ &vertices[15], &vertices[19], 4 },
edge{ &vertices[19], &vertices[20], 5 },
edge{ &vertices[20], &vertices[9], 5 },
edge{ &vertices[1], &vertices[10], 4 },
edge{ &vertices[10], &vertices[11], 2 },
edge{ &vertices[11], &vertices[5], 2 },
edge{ &vertices[2], &vertices[12], 4 },
edge{ &vertices[12], &vertices[14], 4 },
edge{ &vertices[14], &vertices[11], 3 },
edge{ &vertices[11], &vertices[13], 7 },
edge{ &vertices[13], &vertices[6], 2 },
edge{ &vertices[3], &vertices[19], 3 },
edge{ &vertices[19], &vertices[16], 5 },
edge{ &vertices[16], &vertices[17], 2 },
edge{ &vertices[17], &vertices[7], 2 },
edge{ &vertices[4], &vertices[19], 4 },
edge{ &vertices[19], &vertices[17], 6 },
edge{ &vertices[17], &vertices[18], 4 },
edge{ &vertices[18], &vertices[8], 3 }
// Remaining edges are not on routes, and hence are inconsequential and can be omitted
};
// List of routes
std::vector<std::vector<edge*>> routes_arr = {
std::vector<edge*>{ &graph[0], &graph[1], &graph[2], &graph[3], &graph[4] },
std::vector<edge*>{ &graph[5], &graph[6], &graph[7] },
std::vector<edge*>{ &graph[8], &graph[9], &graph[10], &graph[11], &graph[12] },
std::vector<edge*>{ &graph[13], &graph[14], &graph[15], &graph[16] },
std::vector<edge*>{ &graph[17], &graph[18], &graph[19], &graph[20] }
};
std::cout << routes_arr;
// Vdeg list of size V, and initialised
std::vector<vertice_degrees> vertice_degrees_arr;
for(int i = 0; i < vertice_count; i) {
vertice_degrees_arr.push_back(vertice_degrees{ i, 0 });
}
// Add all the routes the vertice is part of for each vertice in Vdeg
for(int i = 0; i < routes_arr.size(); i) {
for(int j = 0, k; j < routes_arr[i].size(); j) {
vertice_degrees& vd = vertice_degrees_arr[routes_arr[i][j]->from->id];
vd.degree = 1;
for(k = 0; k < vd.intersecting.size(); k) {
if(vd.intersecting[k] == i) {
continue;
}
}
vd.intersecting.push_back(i);
}
}
// routes_to_cover is remaining routes left to cover, list of route indexes
std::cout << "\nFilled: \n" << vertice_degrees_arr;
std::vector<int> routes_to_cover;
for(int i = 0; i < routes_arr.size(); i) {
routes_to_cover.push_back(i);
}
// Final resulting S
std::vector<node*> stations_placed_at;
// While there are routes still to cover
while(routes_to_cover.size() > 0) {
// Insertion Sort the Vdeg by degree
for(int i = 1, j; i < vertice_degrees_arr.size(); i) {
const vertice_degrees vd = vertice_degrees_arr[i];
for(j = i; j > 0 && vertice_degrees_arr[j-1] > vd; --j) {
vertice_degrees_arr[j] = vertice_degrees_arr[j-1];
}
vertice_degrees_arr[j] = vd;
}
// Get all the routes intersecting at v, add v to S
std::vector<int> covered_routes = vertice_degrees_arr[vertice_degrees_arr.size()-1].intersecting;
stations_placed_at.push_back(&vertices[ vertice_degrees_arr[vertice_degrees_arr.size()-1].id ]);
std::cout << "\nSorted: \n" << vertice_degrees_arr;
// Remove routes intersecting at v from all Vdeg, decrease degree for next iteration
for(int i = 0; i < vertice_degrees_arr.size(); i) {
for(int j = 0; j < vertice_degrees_arr[i].intersecting.size(); j) {
for(int k = 0; k < covered_routes.size(); k)
if(vertice_degrees_arr[i].intersecting[j] == covered_routes[k]) {
vertice_degrees_arr[i].intersecting.erase(vertice_degrees_arr[i].intersecting.begin() j--);
vertice_degrees_arr[i].degree -= 1;
break;
}
}
}
std::cout << "\nCleaned:\n" << vertice_degrees_arr;
// Remove covered routes this iteration from routes_to_cover
for(int i = 0; i < routes_to_cover.size(); i) {
for(int j = 0; j < covered_routes.size(); j) {
if(routes_to_cover[i] == covered_routes[j]) {
routes_to_cover.erase(routes_to_cover.begin() i--);
break;
}
}
}
print_routes("\nRemaining routes: ", routes_to_cover, routes_arr, "\n");
}
std::cout << "\nFinal Nodes: " << stations_placed_at;
return 0;
}
So what's wrong with this solution?
Is it:
- Not polynomial? or
- Not optimal?
If the former, can you explain how?
If the latter, can you provide a counter?
CodePudding user response:
Your algorithm is not optimal, as can be seen by reduction from the 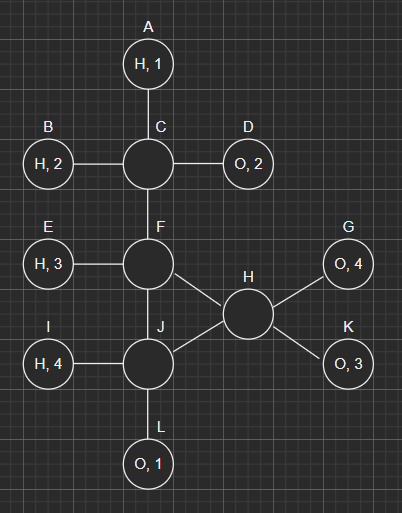
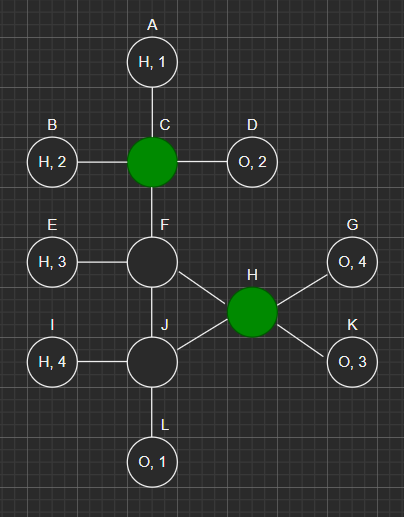
With the following routes:
R1: A, C, F, J, L
R2: B, C, D
R3: E, F, H, K
R4: I, J, H, G
The optimal is selecting the vertices C and H like so:
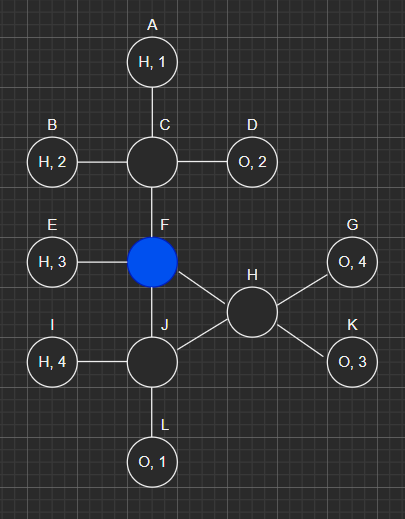
But if our algorithm picks F first (as degrees are same) like so:
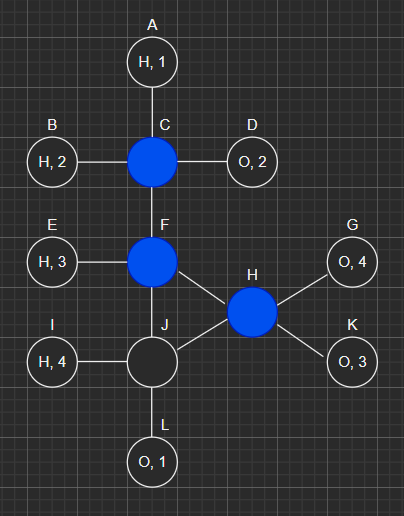
Then we are forced to pick C and one of H or J as follows:
Which is obviously not the optimal solution.