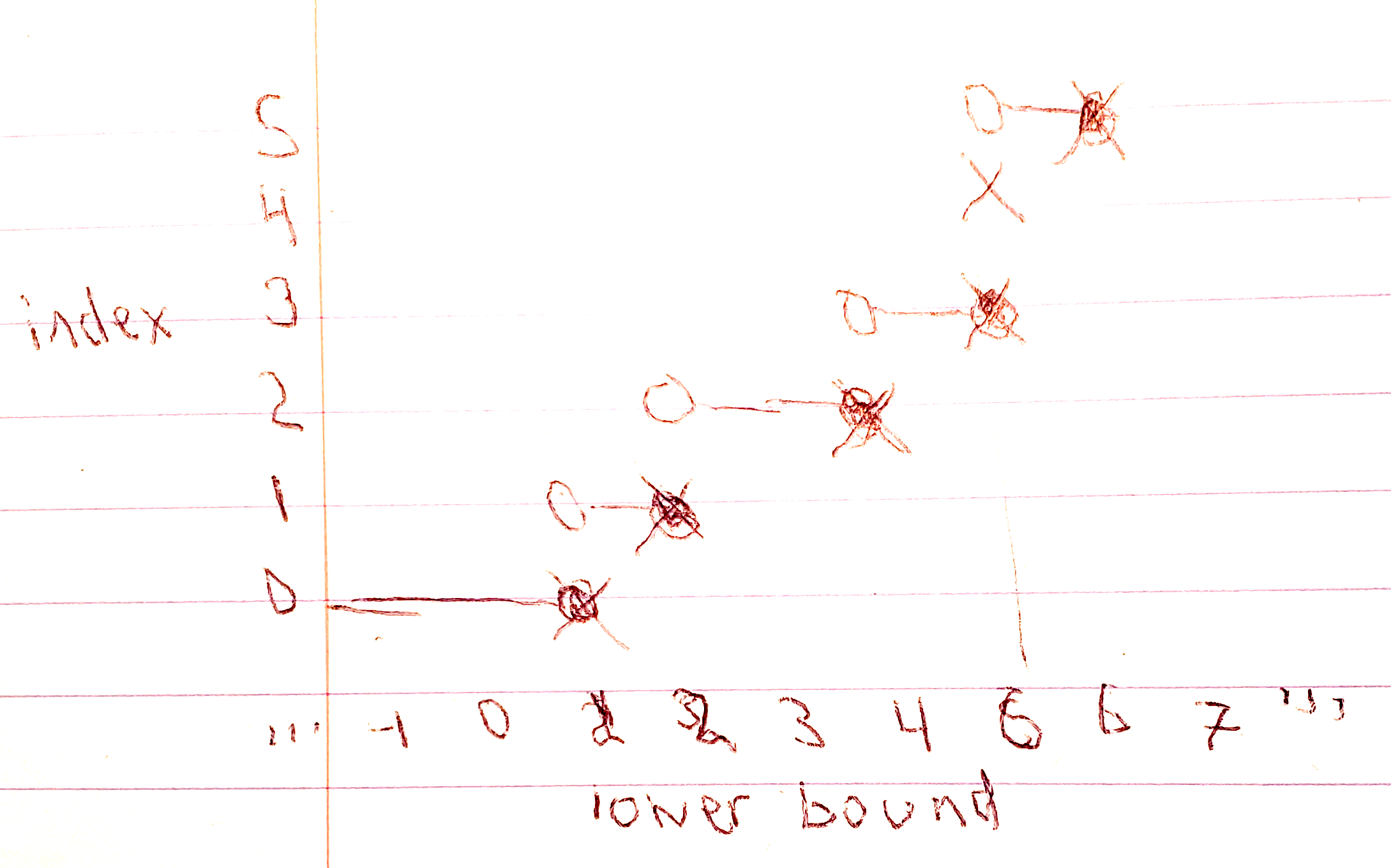Lower bound from the right in a B-tree-CodePudding

I have a B-tree and I'd like to, given an arbitrary parameter key, figure out what the greatest data key less then or equal to the parameter key. In other words, I want it to look to the left to figure out what key it should use in O(log n).

I've already modified the

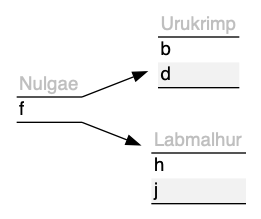
This is not quite what I want. The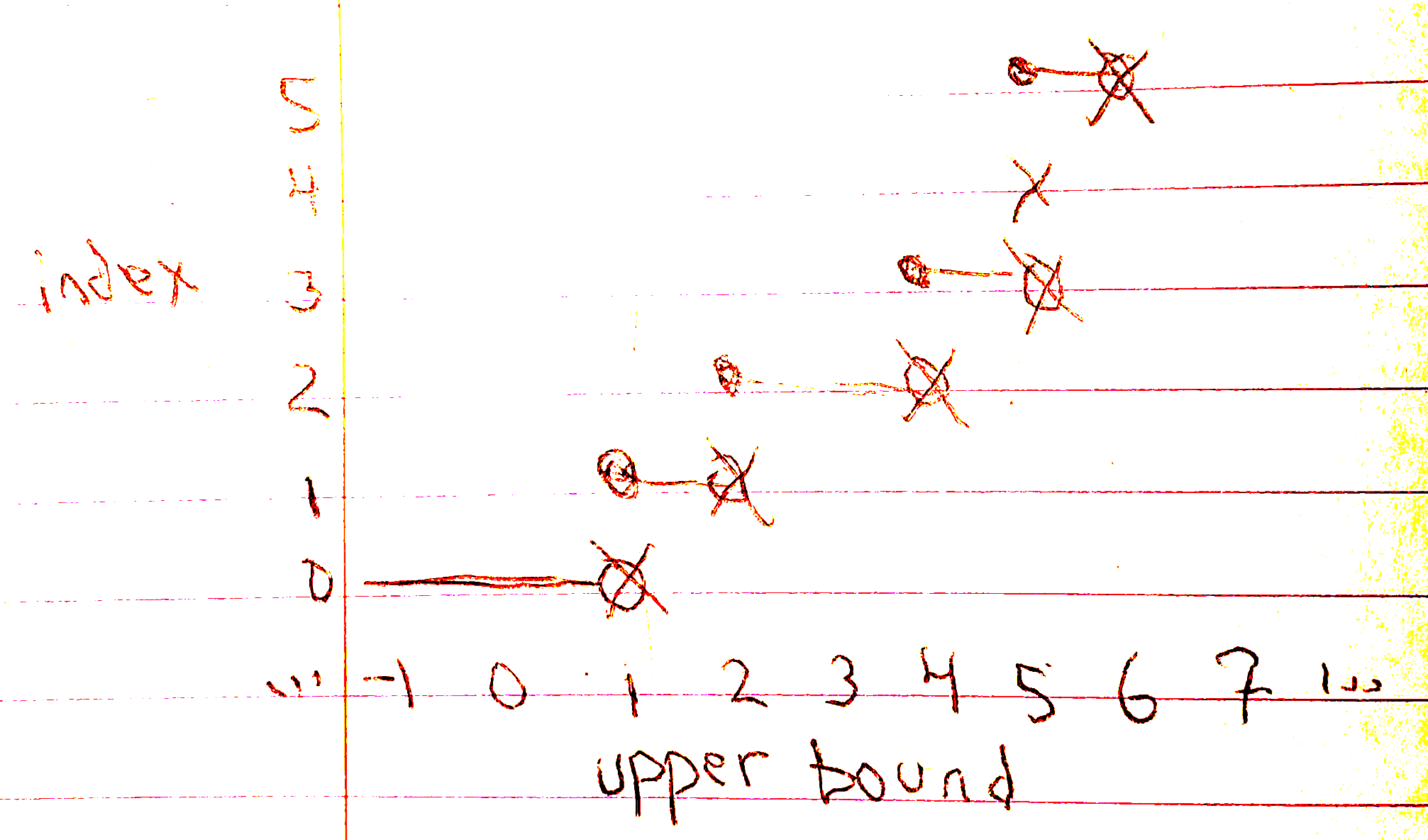

I want a lower bound from the right instead of the left, x->last x in set or 0.

Is there a name for this and how to I modify the lower above to give this result?

CodePudding user response：

The way I would implement this is:

get the upper_bound
get the previous element (if any)
A) if there is a previous element and the element is == the key you are searching for, return it
B) otherwise, return the upper bound

In general you either care about the element directly before the upper_bound or about the upper_bound.

CodePudding user response：

Following the upper_bound advice, I was able to get the required behaviour without going down twice by keeping a return variable that I updated as appropriate. I found that I was being a little sloppy. The lower_bound just lines up correctly, but I found upper_bound not really obvious.

The first thing I did was work out a better example where it would be really obvious what was in the range and what was in the domain. In this case, I thought of the letter keys as the domain and the node-indices as the range, (as in my question.)

Here, key and x are arbitrary elements of the domain of letters. Applying the upper_bound process for each node gives us hi in the range. If hi.idx is non-zero, then found.idx = hi.idx - 1 is an element of the range and a valid data reference. We go down the tree and allow this to be overwritten if appropriate. Finally, in tree_left_or and tree_right_or, we transform the range element found, (it is just an unstable internal pointer-index), to a meaningful corresponding letter domain key in the set of keys.

/* https://github.com/neil-edelman/orcish needed for Graphviz names. */
/*#include "orcish.h"*/
#include <stdio.h>
#include <assert.h>

#define ORDER 3
static int compare(const char a, const char b) { return a > b; }
struct node { unsigned size; char key[ORDER - 1]; };
struct branch { struct node base, *child[ORDER]; };
struct ref { struct node *node; unsigned height, idx; };
struct tree { struct node *node; unsigned height; };

/** @return A reference the element at the greatest lower bound of `x` in
 `tree`, or if the element doesn't exist, `node` will be null. */
static struct ref right(const struct tree tree, const char x) {
    struct ref lo, found;
    found.node = 0;
    if(!tree.node) return found;
    for(lo.node = tree.node, lo.height = tree.height; ;
        lo.node = ((const struct branch *)(const void *)lo.node)->child[lo.idx],
        lo.height--) {
        unsigned hi = lo.node->size; lo.idx = 0;
        if(!hi) continue;
        do {
            const unsigned mid = (lo.idx   hi) / 2; /* Will not overflow. */
            if(compare(x, lo.node->key[mid]) > 0) lo.idx = mid   1;
            else hi = mid;
        } while(lo.idx < hi);
        if(lo.idx < lo.node->size) { /* Within bounds, record the current. */
            found = lo;
            if(compare(x, lo.node->key[lo.idx]) > 0) break;
        }
        if(!lo.height) break;
    }
    return found;
}

/** @return Minimum element equal to or greater then `key` in `tree`, or, if
 the `key` is larger than any in the set, `default_value`. */
static char tree_right_or(const struct tree tree,
    const char key, const char default_value) {
    struct ref ref;
    return (ref = right(tree, key)).node
        && ref.idx < ref.node->size ? ref.node->key[ref.idx] : default_value;
}

/** @return A reference to the predecessor of the element at the least upper
 bound of `x` in `tree`, or `node` will be null if the predecessor doesn't
 exist. */
static struct ref left(const struct tree tree, const char x) {
    struct ref hi, found;
    found.node = 0;
    if(!tree.node) return found;
    for(hi.node = tree.node, hi.height = tree.height; ;
        hi.node = ((const struct branch *)(const void *)hi.node)->child[hi.idx],
        hi.height--) {
        unsigned lo = 0;
        if(!(hi.idx = hi.node->size)) continue;
        do { /* Upper-bound. */
            const unsigned mid = (lo   hi.idx) / 2; /* Will not overflow. */
            if(compare(hi.node->key[mid], x) <= 0) lo = mid   1;
            else hi.idx = mid;
        } while(lo < hi.idx);
        if(hi.idx) {
            found = hi, found.idx--;
            /* Equal elements. */
            if(compare(x, found.node->key[found.idx]) <= 0) break;
        }
        if(!hi.height) break; /* Reached the bottom. */
    }
    return found;
}

/** @return Maximum element equal to or smaller then `key` in `tree`, or, if
 the `key` is smaller than any in the set, `default_value`. */
static char tree_left_or(const struct tree tree,
    const char key, const char default_value) {
    const struct ref ref = left(tree, key);
    return ref.node ? ref.node->key[ref.idx] : default_value;
}

#if 0
static void subgraph(const struct tree *const sub, FILE *fp) {
    const struct branch *branch;
    unsigned i;
    assert(sub->node && fp);
    fprintf(fp, "\ttrunk%p [label = <\n"
        "<table border=\"0\" cellspacing=\"0\">\n"
        "\t<tr><td border=\"0\" port=\"0\">"
        "<font color=\"Gray75\">%s</font></td></tr>\n",
        (const void *)sub->node, orcify(sub->node));
    if(sub->node->size) fprintf(fp, "\t<hr/>\n");
    for(i = 0; i < sub->node->size; i  ) {
        const char *const bgc = i & 1 ? " bgcolor=\"Gray95\"" : "";
        fprintf(fp, "\t<tr><td border=\"0\" align=\"left\""
            " port=\"%u\"%s>%c</td></tr>\n", i   1, bgc, sub->node->key[i]);
    }
    fprintf(fp, "\t<hr/>\n"
        "\t<tr><td></td></tr>\n"
        "</table>>];\n");
    if(!sub->height) return;
    /* Draw the lines between trees. */
    branch = (struct branch *)(void *)sub->node;
    for(i = 0; i <= branch->base.size; i  )
        fprintf(fp, "\ttrunk%p:%u:se -> trunk%p;\n",
        (const void *)sub->node, i, (const void *)branch->child[i]);
    /* Recurse. */
    for(i = 0; i <= branch->base.size; i  ) {
        struct tree child;
        child.node = branch->child[i], child.height = sub->height - 1;
        subgraph(&child, fp);
    }
}
/** <https://graphviz.org/> */
static void graph(const struct tree *const tree,
    const char *const fn) {
    FILE *fp;
    assert(tree && fn);
    if(!(fp = fopen(fn, "w"))) { perror(fn); return; }
    fprintf(fp, "digraph {\n"
        "\tgraph [rankdir=LR, truecolor=true, bgcolor=transparent,"
        " fontname=modern, splines=false];\n"
        "\tnode [shape=none, fontname=modern];\n");
    if(!tree->node)
        fprintf(fp, "\tidle [shape=plaintext];\n");
    else subgraph(tree, fp);
    fprintf(fp, "\tnode [color=\"Red\"];\n"
        "}\n");
    fclose(fp);
}
#endif

int main(void) {
    struct node node[] = { { 2, {'b','d'} }, { 2, {'h','j'} } };
    struct branch root = { { 1, {'f'} }, {node, node 1} };
    const struct tree tree = { &root.base, 1 };
    const int expected[] = { 'z', 'b', 'b', 'd', 'd', 'f',
        'f', 'h', 'h', 'j', 'j', 'j' };
    char left[sizeof expected / sizeof *expected];
    char i;
    int passed;
    /*graph(&tree, "graph.gv");
    printf("nodes in B-tree:\n"
        "%s:(b,d), %s:(f), %s:(h,j)\n\n",
        orcify(&node[0]), orcify(&root), orcify(&node[1]));*/
    printf("right or z\n");
    for(i = 'a'; i < 'm'; i  )
        printf("%c\t%c\n", i, tree_right_or(tree, i, 'z'));
    printf("\n"
        "left or z\n");
    for(i = 'a'; i < 'm'; i  )
        printf("%c\t%c\n", i, left[i-'a'] = tree_left_or(tree, i, 'z'));
    printf("\n"
        "supposed to be...\n");
    for(passed = 1, i = 'a'; i < 'm'; i  ) {
        printf("%c\t%c\n", i, expected[i-'a']);
        if(left[i-'a'] != expected[i-'a']) passed = 0;
    }
    printf("\n"
        "%s.\n", passed ? "PASSED" : "failed");
    return 0;
}