Vectorizing a loop with a "continue" branch in it-CodePudding

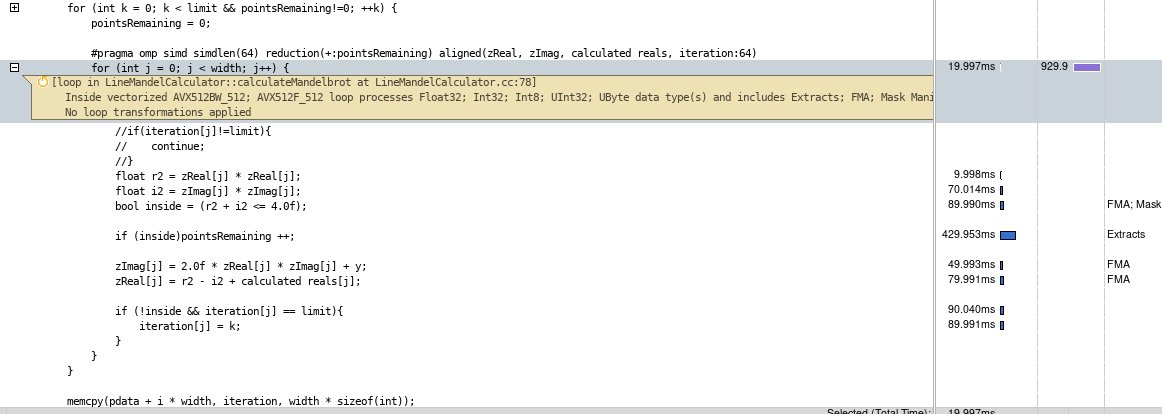
I am currently undergoing a course in which we were given access to a supercomputer. The CPU is an Intel(R) Xeon(R) Gold 6240 CPU. Our task was to vectorize (but we were not allowed to use parallelization) the calculation of mandelbrot set. The goal is to make the code as fast as possible. I tried a number of optimizations. Calculating only the top half of the mandelbrot set then copying the values down, utilizing all possible OpenMP pragmas, and trying to vectorize every loop. My code, however, is way slower than what it is supposed to be (~900ms, while the reference solution is on ~500ms). I need help making this code run much faster. We compile on the icc compiler with these flags -O3 -mavx2 -xHost -g -qopenmp-simd -qopt-report=1 -qopt-report-phase=vec. I ran an Advixe Profiler, and received the following times on the inner loop. However, over multiple runs of the profiler, the times spent on each line varied significantly, though most time was always spent on the pointsRemaining and i2 or r2 variables:

This is my code (it will be run from a custom script - I cannot change the compilation, nor can I change pretty much anything like width or height of the set - but those two will be multiples of 4096, co all aligning is okay). For every line in the image, it computes the iterations (whose number is given by the script that runs the calculator, usually ~100-500). As long as at least one point did not diverge out of the mandelbrot set, the program calculates the iterations for all the points in a line (I tried skipping calculating for every point, but adding the "if" clause that is commented out only slowed down the code - iI think if I manage to vectorize the commented "if", it would run much faster):

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cstring>
#include <stdlib.h>


#include "LineMandelCalculator.h"


LineMandelCalculator::LineMandelCalculator(unsigned matrixBaseSize, unsigned limit) :
    BaseMandelCalculator(matrixBaseSize, limit, "LineMandelCalculator")
{
    data = (int *)(_mm_malloc(height * width * sizeof(int), 64));
    zReal = (float *)(_mm_malloc(width * sizeof(float), 64));
    zImag = (float *)(_mm_malloc(width * sizeof(float), 64));
    iteration = (int *)(_mm_malloc(width * sizeof(int), 64));
    calculated_reals = (float *)(_mm_malloc(width * sizeof(float), 64));


    for (int i = 0; i < width;   i) {
        calculated_reals[i] = x_start   i * dx;
        zReal[i] = 0.0f;
        zImag[i] = 0.0f;
        iteration[i] = limit;
    }
}

LineMandelCalculator::~LineMandelCalculator() {
    _mm_free(data);
    _mm_free(zReal);
    _mm_free(zImag);
    _mm_free(iteration);
    _mm_free(calculated_reals);

    data = NULL;
    zReal = NULL;
    zImag = NULL;
    iteration = NULL;
    calculated_reals = NULL;
}

int * LineMandelCalculator::calculateMandelbrot() {
    int *pdata = data;
    int half_height = height / 2;
    float *zReal = this -> zReal;
    float *zImag = this -> zImag;
    float *calculated_reals = this -> calculated_reals;
    int * iteration = this -> iteration;
    int limit = this -> limit;
    int width = this -> width;
    float dx = (float)this -> dx;
    float dy = (float)this -> dy;

    for (int i = 0; i < half_height; i  ) {
        float y = y_start   i * dy;

        #pragma omp simd simdlen(64) aligned(zReal, zImag, iteration:64)
        for (int j = 0; j < width; j  ) {
            zReal[j] = calculated_reals[j];
            zImag[j] = y;
            iteration[j] = limit;
        }

        int pointsRemaining = width; 

        for (int k = 0; k < limit && pointsRemaining!=0;   k) {
            pointsRemaining = 0; 

            #pragma omp simd simdlen(64) reduction( :pointsRemaining) aligned(zReal, zImag, calculated_reals, iteration:64)
            for (int j = 0; j < width; j  ) {
                //if(iteration[j]!=limit){
                //    continue;
                //}
                float r2 = zReal[j] * zReal[j];
                float i2 = zImag[j] * zImag[j];
                bool inside = (r2   i2 <= 4.0f);

                if (inside)pointsRemaining   ;

                zImag[j] = 2.0f * zReal[j] * zImag[j]   y;
                zReal[j] = r2 - i2   calculated_reals[j];

                if (!inside && iteration[j] == limit){
                    iteration[j] = k;
                }
            }
        }

        memcpy(pdata   i * width, iteration, width * sizeof(int));

        memcpy(pdata   (height - i - 1) * width, pdata   i * width, width * sizeof(int));
    }

    return data;
}

CodePudding user response：

The issue is certainly due to !inside && iteration[j] == limit which needs to be lazily evaluated in C and C . Compilers fail to vectorize such a condition because fetching iteration[j] has a visible behaviour : the compiler cannot evaluate iteration[j] because j might be outside the bounds of iteration based on the value of !inside. As a result, ICC (and other compilers) cannot vectorize the entire loop and generate a slow cascade of conditional jumps.

If you know such a condition can be eagerly evaluated, then you can replace it with (!inside) & (iteration[j] == limit). Expressions using the binary & operator are not lazily evaluated. This enable ICC to generate a fully vectorized code.

That being said, the generated code is huge (about 12 KiB) with 1.5 KiB for the hot loop. A too big code can be detrimental for performance. Indeed, modern x86-64 processors translate instructions to micro-instruction (uops). The translation can often be a bottleneck for hot loops like this. Thus, they have a uops cache not to retranslate instruction but it has a limited size. A too big loop causes the uops cache to miss and instruction to be redecoded over and over which is slow. Regarding the exact target CPU used, it might be an issue or not. On a Intel(R) Xeon(R) Gold 6240 which is a Cascade Lake CPU, I do not expect to be a significant bottleneck. Note that the alignement of the instructions also matter, especially on Cascade Lake (see this post). At first glance, simdlen(64) is why the generated code is so big. It may not be reasonable. At least, certainly not for AVX-2 where simdlen(32) should certainly be preferred.

You specify conflicting compilers flags. Indeed, -xHost tells the compiler to use the available instructions set of the target machine (AFAIK AVX-512 on your target platform) while -mavx2 tells the compiler it can use AVX-2. -mavx2 is thus useless with -xHost. Specify whether you want to use AVX-2 or AVX-512 to the compiler, not both. Your target CPU appear to support 2 AVX-512 units so AVX-512 is the best solution here.

Once vectorized, the code is not bad, but not very efficient either. A very good Mandelbrot implementation should spend most of its time doing FMA instructions. This does not seem the case here. However, it looks like the AVX-512 ALUs are the bottleneck which is quite good. Doing less conditions is certainly something you should try.

The rule of thumb si to look the assembly code generated by your compiler when you are optimizing a code. This si critical. Profiling using low-level tools is also very important. Without that, you are blind and optimization can become very difficult. It can be good to reduce unrolling (simdlen(64) here) in order to get a smaller assembly code that is easier to evaluate (humans can hardly evaluate the quality of assembly codes having thousands of instructions though there are tools can help a lot).

Notes

There are methods to detect points that will never converge. They can be useful to break the iteration loop early when the number of iterations is big.

Iterating over a whole line can make the computation sub optimal if the line does not fit in the L1 cache.

SIMD registers can be used inefficiently if >50% of the items already converged. Reordering items can improve performance a bit when the number of iteration is huge. This is pretty hard to do efficiently in C using OpenMP though.

CodePudding user response：

This is not a complete answer, because it is not completely clear for me, what you are "allowed" to do (e.g., are you allowed to write this manually with intrinsics?) -- and I don't have much experience fudging with OpenMP. But there is a lot that can be optimized with your code.

First of all, the pointsRemaining!=0 condition is essentially useless (it is always true, unless you compute a line which is entirely outside the Mandelbrot set, i.e., if abs(y) > 1.12...).

Checking the condition would make sense however, if you compute smaller tiles. For example, if you compute, 1x16 or 4x4 tiles, which would fit into a register. Then 16 bool inside variables can be merged to a __mmask16 inside_mask, and pointsRemaining!=0 would be equivalent to inside_mask!=0 (which can be checked with a single ktest).

(This essentially answers your continue-Question, only that you would break out of the for(k)-loop instead).

Furthermore,

for(k=0; k<limit;   k) {
   // ...
   if (!inside && iteration[j] == limit){
      iteration[j] = k;
   }
}

is equivalent to starting with iteration[j]=0, and doing

for(k=0; k<limit;   k) {
   // ...
   if(inside)   iteration[j]
}

Assuming you have 16 iteration[] values in a register, this can be done by a single _mm512_mask_add_epi32 (since you have the mask anyway).

Overall, you don't need any zReal, zImag, iteration temporary arrays at all, because all computations can be done entirely in registers (you likely need to calculate with 2 or 4 sets of registers at the same time, to avoid latency-induced bottlenecks). Even the benefit of precomputing calculated_reals is dubious, since the next set of 16 values can be calculated from the previous with a simple vaddps.