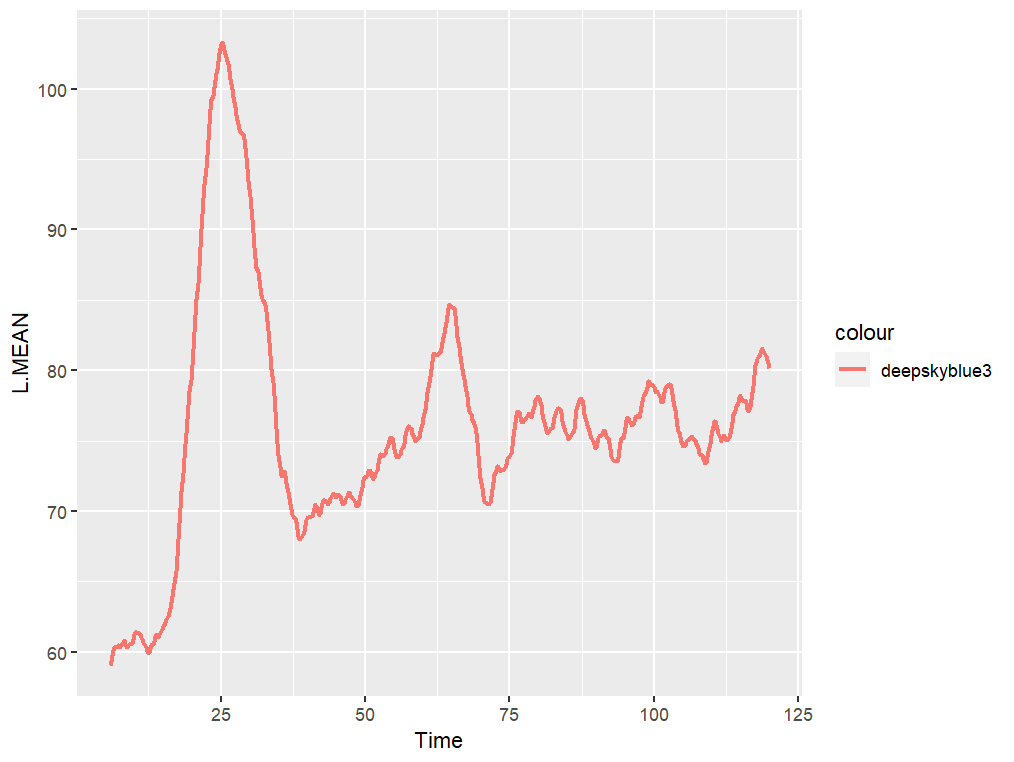
Hi, I have a dataset (and relative plot) that look a bit like this (it's a series of measurements over time). As you can see, it's full of noise (and actually this has already been "smoothed" with a rolling average).
I am trying to achieve 2 things:
Find the first (and highest) peak and the 2 valleys around it. Only this one peak, not all peaks in the curve.
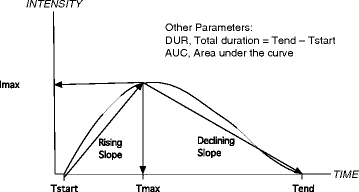
Fit a line from the 1st valley to the peak, and from the peak to the 2nd valley, see example below (I think I have an idea of how to do this, so it's less important)
I've tried some methods found online (like find_peaks from ggpmisc), but I've only been able to find all peaks and valleys, while I only need this specific one (that is the only true one).
Do you guys have any suggestions?
CodePudding user response:
I'll derive some data to analyze:
dat <- data.frame(x = seq(-1, 6*pi, by=0.01))
dat$y <- sin(dat$x) / ifelse(abs(dat$x) < 1e-9, 1, sqrt(abs(dat$x)))
library(ggplot2)
ggplot(dat, aes(x, y)) geom_line()
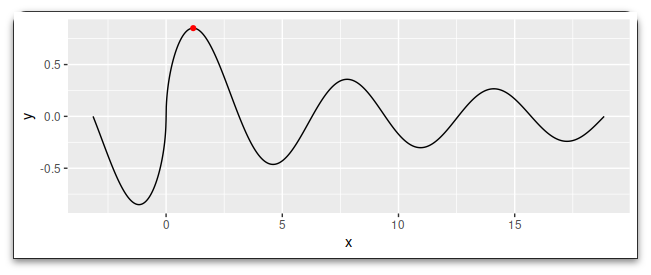
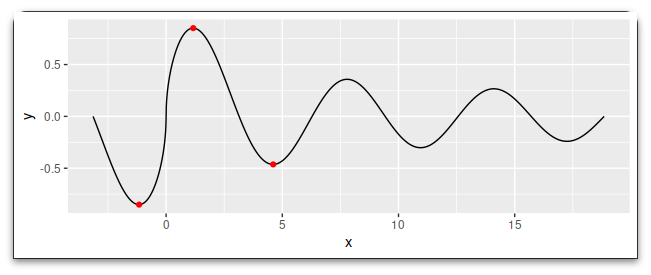
Finding the max is easy with which.max:
ymaxi <- which.max(dat$y)
ymaxi
# [1] 432
dat$y[ymaxi -1:1]
# [1] 0.8512233 0.8512383 0.8511839
ggplot(dat, aes(x, y))
geom_line()
geom_point(data = ~ .[ymaxi,], color = "red")
Finding the preceding/following valleys is a skosh more work
ymini1 <- ymaxi 1L - which(diff(rev(dat$y[1:ymaxi])) > 0)[1]
dat$y[ymini1 -2:2]
# [1] -0.8511520 -0.8512284 -0.8512356 -0.8511732 -0.8510408
ymini2 <- which(diff(dat$y[-(1:ymaxi)]) > 0)[1] ymaxi
dat$y[ymini2 -1:1]
# [1] -0.4633072 -0.4633109 -0.4632688
ggplot(dat, aes(x, y)) geom_line() geom_point(data = ~ .[c(ymini1, ymaxi, ymini2),], color = "red")
I'm defining "valley" as the point where the gradient (diff(.)) changes from negative to positive. You may need to include some tolerance with this, such that the change is held for so-many-points in order to skip false-valleys ... in which case there are a lot of various heuristics, mostly depending on the context of the data and your intent. For instance, you can find the most with a positive above a certain value, such as changing > 0 to > 0.01 or similar, but this can fail if it is positive (sloped-up) but very close to flat. Or you could say look for n-consecutive positives, which is a rolling window question and well-informed by using zoo::rollapply or data.table::frollapply or many other window functions; you could also use run-length-encoding for this (R's rle function), perhaps something like:
diffs <- diff(dat$y[-(1:ymaxi)])
r <- rle(diffs > 0)
r
# Run Length Encoding
# lengths: int [1:6] 343 318 316 315 315 160
# values : logi [1:6] FALSE TRUE FALSE TRUE FALSE TRUE
r$values[r$lengths < 3 & r$values] <- FALSE
which(inverse.rle(r))[1] ymaxi
# [1] 776
which happens to be the same as above, but would "ignore" positive-gradients that are only 1 or 2 points before going negative again.