Complex indexing of a multidimensional array with indices of lower dimensional arrays in Python-CodePudding

Problem:

I have a numpy array of 4 dimensions:
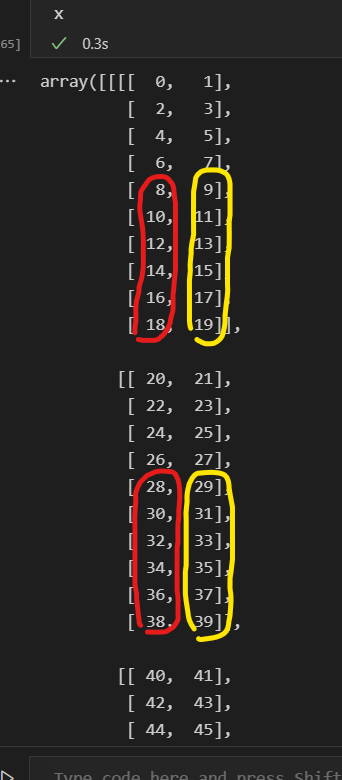
```
x = np.arange(1000).reshape(5, 10, 10, 2 )
```
If we print it:
I want to find the indices of the 6 largest values of the array in the 2nd axis but only for the 0th element in the last axis (red circles in the image):
```
indLargest2ndAxis = np.argpartition(x[...,0], 10-6, axis=2)[...,10-6:]
```
These indices have a shape of (5,10,6) as expected.
I want to obtain the values of the array for these indices in the 2nd axis but now for the 1st element in the last axis (yellow circles in the image). They should have a shape of (5,10,6). Without vectorizing, this could be done with:
```
np.array([ [ [ x[i, j, k, 1] for k in indLargest2ndAxis[i,j]] for j in range(10) ] for i in range(5) ])
```
However, I would like to achieve it vectorizing. I tried indexing with:
```
x[indLargest2ndAxis, 1]
```
But I get IndexError: index 5 is out of bounds for axis 0 with size 5. How can I manage this indexing combination in a vectorized way?

CodePudding user response：

Ah, I think I now get what you are after. Fancy indexing is documented here in detail. Be warned though that - in its full generality - this is quite heavy stuff. In a nutshell, fancy indexing allows you to take elements from a source array (according to some idx) and place them into a new array (fancy indexing allways returns a copy):

source = np.array([10.5, 21, 42])
idx = np.array([0, 1, 2, 1, 1, 1, 2, 1, 0])

# this is fancy indexing
target = source[idx]

expected = np.array([10.5, 21, 42, 21, 21, 21, 42, 21, 10.5])
assert np.allclose(target, expected)

What is nice about this is that you can control the shape of the resulting array using the shape of the index array:

source = np.array([10.5, 21, 42])
idx = np.array([[0, 1], [1, 2]])

target = source[idx]

expected = np.array([[10.5, 21], [21, 42]])
assert np.allclose(target, expected)
assert target.shape == (2,2)

Where things get a little more interesting is if source has more than one dimension. In this case, you need to specify the indices of each axis so that numpy knows which elements to take:

source = np.arange(4).reshape(2,2)
idxA = np.array([0, 1])
idxB = np.array([0, 1])

# this will take (0,0) and (1,1)
target = source[idxA, idxB]

expected = np.array([0, 3])
assert np.allclose(target, expected)

Observe that, again, the shape of target matches the shape of the index used. What is awesome about fancy indexing is that index shapes are broadcasted if necessary:

source = np.arange(4).reshape(2,2)
idxA = np.array([0, 0, 1, 1]).reshape((4,1))
idxB = np.array([0, 1]).reshape((1,2))

target = source[idxA, idxB]

expected = np.array([[0, 1],[0, 1],[2, 3],[2, 3]])
assert np.allclose(target, expected)

At this point, you can understand where your exception comes from. Your source.ndim is 4; however, you try to index it with a 2-tuple (indLargest2ndAxis, 1). Numpy will interpret this as you trying to index the first axis using indLargest2ndAxis, the second axis using 1, and all other axis using :. Clearly, this doesn't work. All values of indLargest2ndAxis would have to be between 0 and 4 (inclusive), since they would have to refer to positions along the first axis of x.

What my suggestion of x[..., indLargest2ndAxis, 1] does is tell numpy that you wish to index the last two axes of x, i.e., you wish to index the third axis using indLargest2ndAxis, the fourth axis using 1, and : for anything else.

This will produce a result since all elements of indLargest2ndAxis are in [0, 10), but will produce a shape of (5, 10, 5, 10, 6) (which is not what you want). Being a bit hand-wavy, the first part of the shape (5, 10) comes from the ellipsis (...), aka. select everything, the middle part (5, 10, 6) comes from indLargest2ndAxis selecting elements along the third axis of x according to the shape of indLargest2ndAxis and the final part (which you don't see because it is squeezed) comes from selecting index 1 along the fourth axis.

Moving on to your actual problem, you can entirely dodge the fancy indexing bullet and do the following:

x = np.arange(1000).reshape(5, 10, 10, 2)
order = x[..., 0]
values = x[..., 1]
idx = np.argpartition(order, 4)[..., 4:]
result = np.take_along_axis(values, idx, axis=-1)

Edit: Of course, you can also use fancy indexing; however, it is more cryptic and doesn't scale as nicely to different shapes:

x = np.arange(1000).reshape(5, 10, 10, 2)
indLargest2ndAxis = np.argpartition(x[..., 0], 4)[..., 4:]
result = x[np.arange(5)[:, None, None], np.arange(10)[None, :, None], indLargest2ndAxis, 1]